题目内容
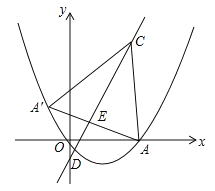
【题目】如图所示，抛物线
经过原点O与点A（6，0）两点，过点A作AC⊥x轴，交直线y=2x﹣2于点C，且直线y=2x﹣2与x轴交于点D．
（1）求抛物线的解析式，并求出点C和点D的坐标；
（2）求点A关于直线y=2x﹣2的对称点A′的坐标，并判断点A′是否在抛物线上，并说明理由；
（3）点P（x，y）是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点Q，设线段PQ的长为l，求l与x的函数关系式及l的最大值．
【答案】（1）
，C（6，10），D（1，0）；（2）A′（﹣2，4），A′在抛物线上；（3）l=
，（﹣2＜x≤6），l的最大值为
．
【解析】
试题分析：（1）把点O（0，0），A（6，0）代入
，得：
，解得：
，∴抛物线解析式为．
当x=6时，y=2×6﹣2=10，当y=0时，2x﹣2=0，解得x=1，∴点C坐标（6，10），点D的坐标（1，0）；
（2）过点A′作AF⊥x轴于点F，∵点D（1，0），A（6，0），可得AD=5，在Rt△ACD中，CD=
=
，∵点A与点A′关于直线y=2x﹣2对称，∴∠AED=90°，∴S△ADC=
×AE=×5×10，解得AE=
，∴AA′=2AE=
，DE=
=
，∵∠AED=∠AFA′=90°，∠DAE=∠A′AF，∴△ADE∽△AA′F，∴
，解得AF=4，A′F=8，∴OF=8﹣6=2，∴点A′坐标为（﹣2，4），当x=﹣2时，y=
，∴A′在抛物线上．
（3）∵点P在抛物线上，则点P（x，
），设直线A′C的解析式为y=kx+b，∵直线A经过A′（﹣2，4），C（6，10）两点，∴
，解得：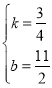
，∴直线A′C的解析式为
，∵点Q在直线A′C上，PQ∥AC，点Q的坐标为（x，
），∵PQ∥AC，又点Q在点P上方，∴l=（
）﹣（）=
，∴l与x的函数关系式为l=，（﹣2＜x≤6），∵l==
，∴当x=
时，l的最大值为．
