Question

【题目】 已知，在中，是边上的一个动点，将沿所在直线折叠，使点落在点处.

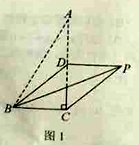
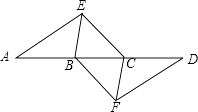
（1）如图1，若点是中点，连接 . ①写出的长；②求证：四边形是平行四边形.

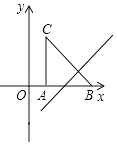
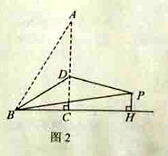
（2）如图2，若，过点作交的延长线于点，求的长.

Answer 1

【答案】（1）①BD=，BP= 2．②证明见解析；（2）．

【解析】

试题分析：（1）①分别在Rt△ABC，Rt△BDC中，求出AB、BD即可解决问题；

②想办法证明DP∥BC，DP=BC即可；

（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=4﹣x，在Rt△BDC中，可得x2=（4﹣x）2+22，推出x=，推出DN=，由△BDN∽△BAM，可得，由此求出AM，由△ADM∽△APE，可得，由此求出AE=，可得EC=AC﹣AE=4﹣=由此即可解决问题．

试题解析：（1）①在Rt△ABC中，∵BC=2，AC=4，

∴AB=，

∵AD=CD=2，

∴BD=，

由翻折可知，BP=BA=2．

②如图1中，

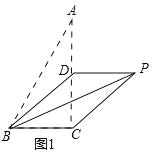
∵△BCD是等腰直角三角形，

∴∠BDC=45°，

∴∠ADB=∠BDP=135°，

∴∠PDC=135°﹣45°=90°，

∴∠BCD=∠PDC=90°，

∴DP∥BC，∵PD=AD=BC=2，

∴四边形BCPD是平行四边形．

（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．

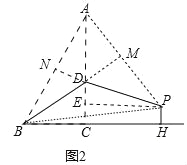
设BD=AD=x，则CD=4﹣x，

在Rt△BDC中，∵BD2=CD2+BC2，

∴x2=（4﹣x）2+22，

∴x=，

∵DB=DA，DN⊥AB，

∴BN=AN=，

在Rt△BDN中，DN=，

由△BDN∽△BAM，可得，

∴

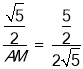
∴AM=2，

∴AP=2AM=4，

由△ADM∽△APE，可得，

∴，

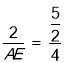∴AE=，

∴EC=AC﹣AE=4﹣=，

易证四边形PECH是矩形，

∴PH=EC=．