题目内容
 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点.
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式和顶点M的坐标,并在给定的直角坐系中画出这条抛物线;
(2)若点(x0,y0)在抛物线上,且1≤x0≤4,写出y0的取值范围;
(3)设平行于y轴的直线x=t交线段BM于点P(点P能与点M重合,不能与点B重合),交x轴于点Q,四边形AQPC的面积为S
①求s关于t的函数关系式及自变量t的取值范围;
②求S取得最大值时P的坐标;
③设四边形OBMC的面积为S’,判断是否存在点P,使得S=S’,若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)本题需先根据抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,即可求出a、b、c的值,从而得出抛物线的解析式,即可求出顶点M的坐标.
(2)本题需先根据抛物线的解析式,分两种情况进行分析,当x0=1时和x0=4时y0的值,即可求出它们的取值范围.
(3)本题需先根据题意设出直线BM的解析式,再把B与M点的坐标代入,求出直线BM的解析式,从而得出P点的坐标,即求出PQ、OQ、OA、OC的值,得出S的解析式;得出解析式后,求出t的值是多少的时候,S最大,得出P点的坐标,求出S的最大值是多少,即可求出S不等于S′,也就是不存在点P.
(2)本题需先根据抛物线的解析式,分两种情况进行分析,当x0=1时和x0=4时y0的值,即可求出它们的取值范围.
(3)本题需先根据题意设出直线BM的解析式,再把B与M点的坐标代入,求出直线BM的解析式,从而得出P点的坐标,即求出PQ、OQ、OA、OC的值,得出S的解析式;得出解析式后,求出t的值是多少的时候,S最大,得出P点的坐标,求出S的最大值是多少,即可求出S不等于S′,也就是不存在点P.
解答: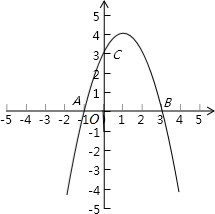 解:(1)∵抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3),
解:(1)∵抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3),
∴
∴
∴抛物线的解析式是:y=-x2+2x+3
∴抛物线的顶点M的坐标是(1,4)
(2)∵抛物线的解析式是y=-x2+2x+3,
当x0=1时,y0=4
当x0=4时,
y0=-5,
∴当1≤x0≤4时,-5≤y0≤4
(3)①设直线BM的解析式为y=mx+n
把B(3,0),M(1,4)代入得
,
∴
∴直线BM的解析式为:y=-2x+6,
∴P点的坐标为:(t,-2t+6),
∴PQ=|-2t+6|=-2t+6,
又OQ=|t|=t OA=|-1|=1,OC=|3|=3,
∴S=S△AOC+S梯形OQPC
=
×OA×OC+
(OC+PQ)×OQ
=
×1×3+
×(3-2t+6)×t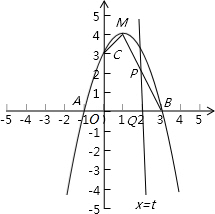
=-t2+
t+
(1≤t<3)
②S=-t2+
t+
=-(t2-
t-
)
=-(t-
)2+2+
∴当t=
时,S最大,
∴S的最大值为
,这时P点坐标为(
,
)
③S=
×(3+4)×1+
×2×4
=
+4
=
∴S的最大值为
<
∴S=S′不可能,
∴不存在点P,使S=S′.
 解:(1)∵抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3),
解:(1)∵抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3),∴
|
∴
|
∴抛物线的解析式是:y=-x2+2x+3
∴抛物线的顶点M的坐标是(1,4)
(2)∵抛物线的解析式是y=-x2+2x+3,
当x0=1时,y0=4
当x0=4时,
y0=-5,
∴当1≤x0≤4时,-5≤y0≤4
(3)①设直线BM的解析式为y=mx+n
把B(3,0),M(1,4)代入得
|
∴
|
∴直线BM的解析式为:y=-2x+6,
∴P点的坐标为:(t,-2t+6),
∴PQ=|-2t+6|=-2t+6,
又OQ=|t|=t OA=|-1|=1,OC=|3|=3,
∴S=S△AOC+S梯形OQPC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |

=-t2+
| 9 |
| 2 |
| 3 |
| 2 |
②S=-t2+
| 9 |
| 2 |
| 3 |
| 2 |
=-(t2-
| 9 |
| 2 |
| 3 |
| 2 |
=-(t-
| 9 |
| 4 |
| 105 |
| 16 |
∴当t=
| 9 |
| 4 |
∴S的最大值为
| 105 |
| 16 |
| 9 |
| 4 |
| 3 |
| 2 |
③S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 7 |
| 2 |
=
| 15 |
| 2 |
∴S的最大值为
| 105 |
| 16 |
| 105 |
| 16 |
| 15 |
| 2 |
∴S=S′不可能,
∴不存在点P,使S=S′.
点评:本题主要考查了二次函数综合问题,在解题时要涉及到的知识点有抛物线的顶点公式和取值范围以及最大值问题,在求有关最值问题时要注意分析题意分情况讨论结果.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=