题目内容
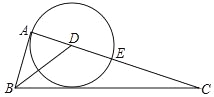
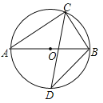
【题目】如图,AB为⊙O的直径,C为圆上(除A、B外)一动点,∠ACB的角平分线交⊙O于D,若AC=8,BC=6,则BD的长为______.
【答案】![]() .
.
【解析】
根据圆周角定理,由AB为⊙O直径得到∠ACB=90°,则可根据勾股定理计算出AB=10,接着根据圆周角定理得到∠ABD=∠ACD=45°, ∠BAD=∠BCD=45°,于是可判断△ADB为等腰直角三角形,然后根据等腰直角三角形的性质求AD.
解: ∵ AB为⊙O直径,
∴∠ACB=90°,
在Rt△ACB中, ∵AC=8,BC=6,
∴AB=![]() ,
,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠ABD=∠ACD=45°, ∠BAD=∠BCD=45°,
∴△ADB为等腰直角三角形,
∴AD=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目