题目内容
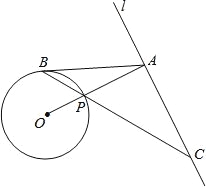
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=![]() ,OA=3,求⊙O的半径和线段PB的长.
,OA=3,求⊙O的半径和线段PB的长.
【答案】(1)证明详见解析;(2)![]() .
.
【解析】
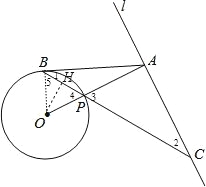
试题分析:(1)连结OB,如图,由等腰三角形的性质得∠1=∠2,∠4=∠5,由OA⊥AC得∠2+∠3=90°,加上∠3=∠4,易得∠5+∠1=90°,即∠OBA=90°,于是根据切线的判定定理可得AB是⊙O的切线;
(2)作OH⊥PB于H,如图,根据垂径定理得到BH=PH,设⊙O的半径为r,则PA=OA﹣OP=3﹣r,根据勾股定理得到![]() ,
,![]() ,所以
,所以![]() ,解得r=1,则PA=2,然后证明Rt△APC∽Rt△HPO,利用相似比可计算出PH=
,解得r=1,则PA=2,然后证明Rt△APC∽Rt△HPO,利用相似比可计算出PH=![]() ,于是得到PB=2PH=
,于是得到PB=2PH=![]() .
.
试题解析:(1)连结OB,如图,
∵AB=AC,
∴∠1=∠2,
∵OA⊥AC,
∴∠2+∠3=90°,
∵OB=OP,
∴∠4=∠5,
而∠3=∠4,
∴∠5+∠2=90°,
∴∠5+∠1=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)作OH⊥PB于H,如图,则BH=PH,
设⊙O的半径为r,则PA=OA﹣OP=3﹣r,
在Rt△PAC中,![]() ,
,
在Rt△OAB中,![]() ,
,
而AB=AC,
∴![]() ,解得r=1,
,解得r=1,
即⊙O的半径为1;
∴PA=2,
∵∠3=∠4,
∴Rt△APC∽Rt△HPO,
∴![]() ,即
,即![]() ,
,
∴PH=![]() ,
,
∴PB=2PH=![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?