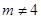题目内容
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且 .
.

(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出;
(3)方程 的解;
的解;
(4)使一次函数的值大于反比例函数的值的 的取值范围;
的取值范围;
 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出;
(3)方程
 的解;
的解;(4)使一次函数的值大于反比例函数的值的
 的取值范围;
的取值范围;(1) ,
, ;(2)A(-1,3),C(3,-1),
;(2)A(-1,3),C(3,-1), ;(3)
;(3) ;(4)
;(4) 或
或
 ,
, ;(2)A(-1,3),C(3,-1),
;(2)A(-1,3),C(3,-1), ;(3)
;(3) ;(4)
;(4) 或
或
试题分析:(1)先根据反比例函数系数k的几何意义求得k的值,即可求得结果;
(2)先求出两个图象的交点坐标,以及一次函数与x轴的交点坐标,再根据三角形的面积公式求解;
(3)根据函数图象上的点的坐标的特征结合函数图象的特征求解即可;
(4)找到一次函数的图象在反比例函数的图象上方的部分对应的
 的取值范围即可.
的取值范围即可.解:(1)因为

所以
 ,解得
,解得
因为图象在第二、四象限,
所以
 ,
,所以反比例函数解析式为
 ,一次函数解析式为:
,一次函数解析式为: ;
;(2)由
 解得
解得 或
或 ,则A(-1,3),C(3,-1)
,则A(-1,3),C(3,-1)在
 中,当
中,当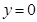 时,
时, ,
,
所以△AOC的面积
 ;
;(3)由题意得方程
 的解为
的解为 ;
;(3)当
 或
或 时,一次函数的值大于反比例函数的值.
时,一次函数的值大于反比例函数的值.点评:此类问题是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 中,自变量x的取值范围是【 】
中,自变量x的取值范围是【 】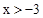



 ,有一个关于x的函数,不论x取何值,y的解析式总是取y1、y2、y3中的值的较小的一个,则y的最大值等于
,有一个关于x的函数,不论x取何值,y的解析式总是取y1、y2、y3中的值的较小的一个,则y的最大值等于 





 中,
中, 的取值范围是
的取值范围是 ,则
,则 为( )
为( )