题目内容
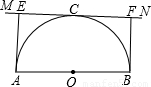
(2000•兰州)如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F.求证:(1)AE+BF=AB;(2)EF2=4AE•BF.
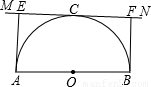
【答案】分析:(1)连接OC,先利用AE、BF都垂直于MN,而AB≠EF,可证四边形ABFE是梯形,而O是AB中点,且AE∥OC∥BF,利用平行线分线段成比例定理的推论,易得CE:CF=AO:BO,那么C也是EF中点,从而OC使梯形中位线,利用梯形中位线定理可证AE+BF=2OC,而AB=2OC,即可证;
(2)连接AC、BC,AB是直径,易得∠ACB是90°,从而∠ACE+∠FCB=90°,而BF⊥MN,易得∠FCB+∠FBC=90°,利用同角的余角相等,可证∠ECA=∠FBC,再加上一对直角相等,容易证出△EAC∽△FCB,可得比例线段,再结合CE=CF= EF,代入比例线段,化简即可得证.
EF,代入比例线段,化简即可得证.
解答: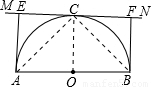 证明:(1)连接OC,
证明:(1)连接OC,
∵AE⊥MN,BF⊥MN,
∴AE∥BF,而AB≠EF,
∴四边形ABFE为梯形,(1分)
∵OC∥AE∥BF,
∴EC=CF,
∴OC为梯形ABFE的中位线,
∴AE+BF=2OC,
即:AE+BF=AB.(2分)
(2)连接AC、BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ECA+∠FCB=90°,
∵∠CBF+∠FCB=90°,
∠CBF=∠ECA,
∴△AEC∽△CFB,
∴CF•EC=AE•BF,(1分)
∵CF=EC= EF,(1分)
EF,(1分)
∴EF2=4AE•BF.(1分)
点评:本题利用了梯形的判定、平行线分线段成比例定理的推论、梯形中位线定理、同角的余角相等、相似三角形的判定和性质等知识.
(2)连接AC、BC,AB是直径,易得∠ACB是90°,从而∠ACE+∠FCB=90°,而BF⊥MN,易得∠FCB+∠FBC=90°,利用同角的余角相等,可证∠ECA=∠FBC,再加上一对直角相等,容易证出△EAC∽△FCB,可得比例线段,再结合CE=CF=
 EF,代入比例线段,化简即可得证.
EF,代入比例线段,化简即可得证.解答:
 证明:(1)连接OC,
证明:(1)连接OC,∵AE⊥MN,BF⊥MN,
∴AE∥BF,而AB≠EF,
∴四边形ABFE为梯形,(1分)
∵OC∥AE∥BF,
∴EC=CF,
∴OC为梯形ABFE的中位线,
∴AE+BF=2OC,
即:AE+BF=AB.(2分)
(2)连接AC、BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ECA+∠FCB=90°,
∵∠CBF+∠FCB=90°,
∠CBF=∠ECA,
∴△AEC∽△CFB,
∴CF•EC=AE•BF,(1分)
∵CF=EC=
 EF,(1分)
EF,(1分)∴EF2=4AE•BF.(1分)
点评:本题利用了梯形的判定、平行线分线段成比例定理的推论、梯形中位线定理、同角的余角相等、相似三角形的判定和性质等知识.

练习册系列答案
相关题目