题目内容
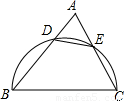
（2000•兰州）如图，已知半圆O，交AB于D、AC于E，BC是直径，若∠A=60°，AB=16，AC=10，求AD、AE、DE的长．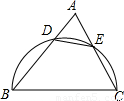
【答案】分析：连接CD，由圆周角定理知CD⊥AB；Rt△ACD中，易知∠ACD=30°，根据直角三角形的性质即可求得AD、CD的长；进而可在Rt△CDB中，由勾股定理求出BC的长；然后证△ADE∽△ACB，通过相似三角形得出的成比例线段求得AE、BC的长．
解答：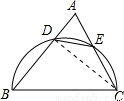
解：连接CD，则∠CDB=90°；
Rt△ACD中，∠ACD=30°，AC=10，
则AD=5，CD=5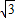
；
Rt△BCD中，BD=AB-AD=11，CD=5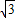
，
由勾股定理，得：BC=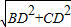
=14；
∵四边形BCED是圆的内接四边形，
∴∠ADE=∠C，∠AED=∠B；
∴△ADE∽△ABC
∴
=
=
；
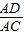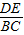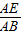∴DE=AD•BC÷AC=5×14÷10=7，
AE=AD•AB÷AC=5×16÷10=8．
点评：此题主要考查了圆周角定理、解直角三角形以及相似三角形的判定和性质等知识的综合应用能力．
解答：
解：连接CD，则∠CDB=90°；Rt△ACD中，∠ACD=30°，AC=10，
则AD=5，CD=5
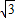；Rt△BCD中，BD=AB-AD=11，CD=5
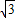，由勾股定理，得：BC=
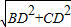=14；∵四边形BCED是圆的内接四边形，
∴∠ADE=∠C，∠AED=∠B；
∴△ADE∽△ABC
∴
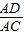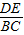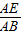==；∴DE=AD•BC÷AC=5×14÷10=7，
AE=AD•AB÷AC=5×16÷10=8．
点评：此题主要考查了圆周角定理、解直角三角形以及相似三角形的判定和性质等知识的综合应用能力．
练习册系列答案
阅读快车系列答案
相关题目
