题目内容
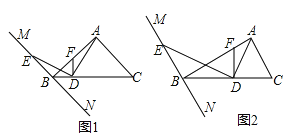
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
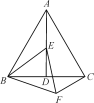
(1)求证:AE=CF;
(2)求∠ACF的度数.
【答案】(1)证明见解析;(2)∠ACF=90°.
【解析】
(1)根据△ABC是等边三角形,得出AB=BC,∠ABE+∠EBC=60°,再根据△BEF是等边三角形,得出EB=BF,∠CBF+∠EBC=60°,从而求出∠ABE=∠CBF,最后根据SAS证出△ABE≌△CBF,即可得出AE=CF;
(2)根据△ABC是等边三角形,AD是∠BAC的角平分线,得出∠BAE=30°,∠ACB=60°,再根据△ABE≌△CBF,得出∠BCF=∠BAE=30°,从而求出∠ACF的度数.
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60 °.
∵△BEF是等边三角形,
∴EB=BF,∠CBF+∠EBC=60 °.
∴∠ABE=∠CBF.
在△ABE和△CBF中,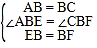 ,
,
∴△ABE≌△CBF(SAS).
∴AE=CF;
(2)∵等边△ABC中,AD是∠BAC的角平分线,
∴∠BAE=![]() ∠BAC=30 °,∠ACB=60°.
∠BAC=30 °,∠ACB=60°.
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30 °.
∴∠ACF=∠BCF+∠ACB=30 °+60 °=90 °.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目