题目内容
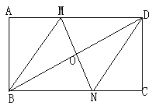
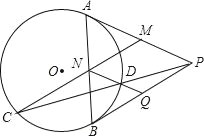
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
【答案】见解析
【解析】试题分析:连接OA,OB,OC,OD,OP. 由![]() 是
是![]() 的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为
的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为![]() 的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
MP∥NQ,则可得四边形MNQP是平行四边形,证得四边形MNQP是菱形.
试题解析:证明:连接OA,OB,OC,OD,OP.
∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB为![]() 的切线,
的切线,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得![]()
由切割线定理,得![]()
∴PNPO=PDPC,
∴O,C,D,N四点共圆,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四边形MNQP是平行四边形,
∴四边形MNQP是菱形.

练习册系列答案
相关题目