题目内容
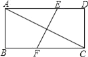
【题目】如图,在矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E、交BC于点F,则EF的长为( )
A. 4 B. 2![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】
过D作DK平行EF交CF于K,得出平行四边形DEFK,推出EF=DK,证△DCK∽△CBA,求出CK,根据勾股定理求出DK即可.
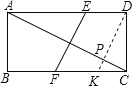
过D作DK平行EF交CF于K,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠DCB=90°,AD=BC=4,AB=CD=2,
∵AD∥BC,EF∥DK,
∴DEFK为平行四边形,
∴EF=DK,
∵EF⊥AC,
∴DK⊥AC,
∴∠DPC=90°,
∵∠DCB=90°,
∴∠CDK+∠DCP=90°,∠DCP+∠ACB=90°,
∴∠CDK=∠ACB,
∵∠DCK=∠ABC=90°,
∴△CDK∽△BCA,
∴![]() ,
,
即![]() ,
,
CK=1,
根据勾股定理得:EF=DK=![]() ,
,
故选:C.

练习册系列答案
相关题目