题目内容
【题目】如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
【答案】
(1)
证明:在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,
∴BE=DC,
∴四边形BECD为平行四边形,
∴BD=EC.
∴在△ABD与△BEC中,
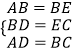 ,
,
∴△ABD≌△BEC(SSS)
(2)
证明:由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴OC+OB=OD+OE,即BC=ED,
∴平行四边形BECD为矩形
【解析】(1)由平行四边形ABCD,易得四边形BECD为平行四边形,然后由SSS推出两三角形全等即可;(2)由(1),易证得BC=ED,即可证得四边形BECD是矩形.
【考点精析】本题主要考查了平行四边形的性质和矩形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.

练习册系列答案
相关题目