题目内容
(1)对角线互相垂直平分的四边形是________.
(2)一个菱形的两条对角线长分别为6cm,8cm,这个菱形的边长为________,面积________.
(3)菱形的周长为48cm,一条对角线长是12cm,则菱形相邻的两个内角是________.
(4)矩形四边中点所确定的四边形是________.
(5)菱形的周长为20cm,两邻角的比为1∶2,则它的面积是________.
答案:略
解析:
解析:
|
(1) 对角线互相平分的四边形是平行四边形,又因对角线互相垂直的平行四边形是菱形,所以,对角线互相垂直平分的四边形是菱形.(2) 如图所示,由已知画图得,AC=8cm,BD=6cm
∵四边形 ABCD为菱形∴ 
∠ AOD=90°∴ 
(3) 如图所示
∵四边形 ABCD为菱形∴ 
又∵ BD=12∴△ ABD为等边三角形∴∠ A=60°又∵ AD∥BC∴∠ ABC=180°-60°=120°∴相邻两角分别为 60°,120°(4) 由已知画图所示
E 、F、G、H分别为AB、BC、CD、DA的中点连接AC、BD∵ E、F分别为AB、AD的中点∴  . .
同理得 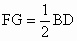 , ,
又∵四边形 ABCD为矩形∴ AC=BD∴ EF=FG=HG=EH∴矩形四边中点所确定的四边形是菱形. (5) 由已知画图所示,连接AC、BD交于O
∵四边形 ABCD为菱形∴ 
AD ∥BC∴∠ DAB+∠ABC=180°又∵∠ DAB∶∠ABC=1∶2∴∠ DAB=60°∴△ ABD为等边三角形∴ BD=5(cm).又∵ OD=OB,∴OD=2.5(cm)∵ AC⊥BD ∴
∴ 
∴ 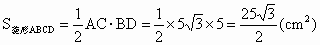 |

练习册系列答案
相关题目





