题目内容
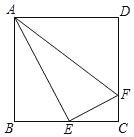
【题目】如图,正方形ABCD中,E是BC的中点,F为CD上一点,CD=4CF,下列结论:
(1)∠BAE=30°;
(2)AE⊥EF;
(3)AE=2EF,其中正确的个数为( )
A.0个B.1个C.2个D.3个
【答案】C
【解析】
根据正方形性质、相似三角形应用以及三角函数逐一求证即可
解:如图所示:
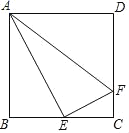
(1))∠BAE=30°是错误的,其原因如下:
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠C=90°
又∵E是BC的中点,
∴BE=CE=![]() BC=
BC=![]() AB,
AB,
又∵在Rt△ABE中,tan∠BAE=![]() =
=![]() ,
,
tan30°=![]() ,
,
∴![]()
∴∠BAE<30°,
∴(1)不正确;
(2)AE⊥EF是正确的,其原因如下:
∵CD=4CF,
∴CD=2CE,
∵![]() ,∠B=∠C=90°,
,∠B=∠C=90°,
∴△ABE∽△ECF,
∴∠BAE=∠CEF,
又∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
又∵∠BEA+∠AEF+∠CEF=180°,
∴∠AEF=90°,
∴AE⊥EF,
∴(2)正确.
(3)AE=2EF正确,其原因如下:
∵由(2)可知△ABE∽△ECF,
∴![]()
∴AE=2EF,
所以③正确;
综合所述,(2)(3)正确.
故选:C.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目