Question

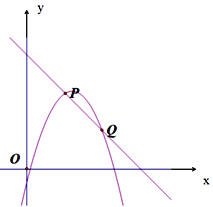
【题目】已知：如图，直线y=-x+b与抛物线y=-x2+4x+c交于P、Q两点．

（1）若点P坐标为（1，2），

①求c的值；

②求Q点坐标；

（2）若 P、Q两点的横坐标分别为m、n，且0<m<n．分别过点P、Q作PA、QB垂直于x轴，垂足分别为点A、B．当△AOP≌△BQO时．

①求m+n的值；

②求证：

Answer 1

【答案】(1)①c=-1；②（4，-1）；(2)①m+n=5；②证明见解析

【解析】

（1）将P（1，2）代入即可解题,（2）根据全等得P（m,n）,Q(n,m),联立方程即可求解,再利用根的判别式即可判定c的取值范围.

解：（1）将P（1，2）代入y=-x2+4x+c中得c=-1, 将P（1，2）代入y=-x+b中得b=3,

∴直线为y=-x+3,抛物线为y=-x2+4x-1,

联立方程组 解得： 或,

∴Q（4，-1）；

（2）①如下图,∵△AOP≌△BQO,

∴OA=BQ,AP=OB,即P（m,n）,Q(n,m),

∵P,Q两点都在函数y=-x2+4x-1上,即,

（2）-（1）得m+n=5,

②∵m=5-n,将m代入方程中得n2-5n+5-c=0,

∴△0,解得c,当c时P,Q重合,直线与抛物线只有一个交点,

∴