题目内容
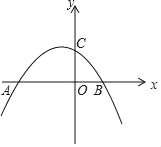
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
(1)求抛物线的函数解析式并直接写出顶点M坐标;
(2)连接AM,N是AM的中点,连接BN,求线段BN长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
【答案】(1)(-1,![]() ,)(2)
,)(2)![]()
【解析】
(1)利用交点式写出抛物线解析式,然后把解析式配成顶点式得到M点的坐标;
(2)利用线段中点坐标公式得到N点坐标,然后利用两点间的距离公式计算BN的长.
(1)抛物线解析式为y=﹣![]() (x+4)(x﹣2),
(x+4)(x﹣2),
即y=﹣![]() x2﹣
x2﹣![]() x+2,
x+2,
∵y=﹣![]() (x+1)2+
(x+1)2+![]() ,
,
∴抛物线的顶点坐标为(﹣1,![]() );
);
(2)∵N是AM的中点,
∴M点的坐标为(﹣![]() ,
,![]() ),
),
∴BN=![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
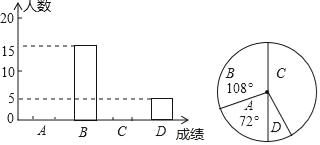
【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?