��Ŀ����
����Ŀ������ij��ͬѧС�������ѧϰ�����ľ��飬ͨ���о�һ��δѧ���ĺ�����ͼ�Ӷ�̽������������ʣ�
�±��Ǻ���y���Ա���x�ļ����Ӧֵ��
x | �� | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | �� |
y | �� | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | �� |
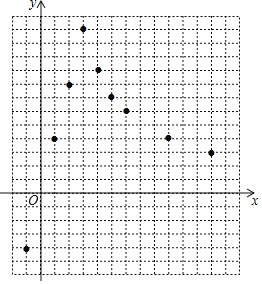
��1����ƽ��ֱ������ϵxOy�У�ÿ��С�����εı߳�Ϊһ����λ���ȣ���������ϱ��и��Զ�ӦֵΪ����ĵ㣬���������ĵ㣬�����ú�����ͼ��
��2������ݻ����ĺ���ͼ��ֱ��д���ú����Ĺ�ϵʽy=______����д���Ա�����ȡֵ��Χ������д���ú�����һ�����ʣ�______��
��3����ֱ��y=-![]() x+b��ú���ͼ����3������ʱ����b��ȡֵ��Χ��
x+b��ú���ͼ����3������ʱ����b��ȡֵ��Χ��
���𰸡���1����������2����x��3ʱ��k=4��0������x������yֵ����3����4��b��9ʱ�����к���ͼ����3������
��������
��1�������б������ɻ���������ͼ��
��2�����ݺ���ͼ��x��3ʱ������Ϊ��������������x��3ʱ������Ϊ������������
��3�����ݺ�����ͼ����ͨ��ƽ�����b��ֵ��
��1��
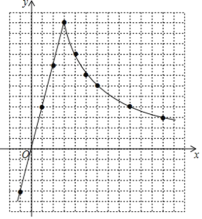
��2����x��3ʱ������Ϊ��������������1��4������y=kx�����k=4��y=4x��
��x��3ʱ������Ϊ��������������6��6������y=![]() �����k=36��y=
�����k=36��y=![]() ��
��
�ߵ�x��3ʱ��k=4��0��
������x����yֵ����
�ʴ�Ϊ��y=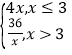 ����x��3ʱ��k=4��0��y����x�����������
����x��3ʱ��k=4��0��y����x�����������
��3����ͼ���֪����4��b��9ʱ�����к���ͼ����3�����㣮

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�