Question

【题目】已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．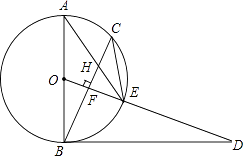
（1）求证：BD是⊙O的切线；
（2）求证：CE2=EHEA；
（3）若⊙O的半径为 ，sinA= ，求BH的长．

Answer 1

【答案】
（1）证明：如图1中，

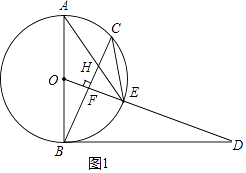
∵∠ODB=∠AEC，∠AEC=∠ABC，

∴∠ODB=∠ABC，

∵OF⊥BC，

∴∠BFD=90°，

∴∠ODB+∠DBF=90°，

∴∠ABC+∠DBF=90°，

即∠OBD=90°，

∴BD⊥OB，

∴BD是⊙O的切线；

（2）证明：连接AC，如图2所示：

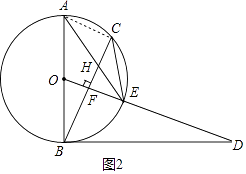
∵OF⊥BC，

∴ = ，

∴∠CAE=∠ECB，

∵∠CEA=∠HEC，

∴△CEH∽△AEC，

∴ = ，

∴CE2=EHEA；

（3）解：连接BE，如图3所示：

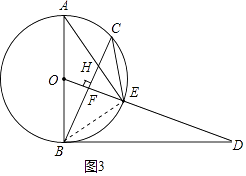
∵AB是⊙O的直径，

∴∠AEB=90°，

∵⊙O的半径为 ，sin∠BAE= ，

∴AB=5，BE=ABsin∠BAE=5× =3，

∴EA= =4，

∵ = ，

∴BE=CE=3，

∵CE2=EHEA，

∴EH= ，

∴在Rt△BEH中，BH= = =

【解析】（1）如图1中，欲证明BD是切线，只要证明AB⊥BD即可；（2）连接AC，如图2所示，欲证明CE2=EHEA，只要证明△CEH∽△AEC即可；（3）连接BE，如图3所示，由CE2=EHEA，可得EH= ，在Rt△BEH中，根据BH= ，计算即可；