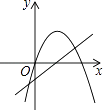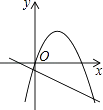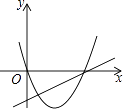题目内容
【题目】（1）如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．
求证：△BEC≌△CDA；
（模型应用）
（2）①已知直线l1：y=
x+4与坐标轴交于点A、B，将直线l1绕点A逆时针旋转45o至直线l2，如图2，求直线l2的函数表达式；
②如图3，长方形ABCO，O为坐标原点，点B的坐标为（8，-6），点A、C分别在坐标轴上，点P是线段BC上的动点，点D是直线y=-2x+6上的动点且在第四象限．若△APD是以点D为直角顶点的等腰直角三角形，请直接写出点D的坐标．
【答案】⑴证明见解析；⑵y=-7x-21；⑶D（4，-2），（
，
）.
【解析】
（1）根据△ABC为等腰直角三角形，AD⊥ED，BE⊥ED，可判定△ACD≌△CBE；
（2）①过点B作BC⊥AB，交l2于C，过C作CD⊥y轴于D，根据△CBD≌△BAO，得出BD=AO=3，CD=OB=4，求得C（-4，7），最后运用待定系数法求直线l2的函数表达式；
②根据△APD是以点D为直角顶点的等腰直角三角形，当点D是直线y=-2x+6上的动点且在第四象限时，分两种情况：当点D在矩形AOCB的内部时，当点D在矩形AOCB的外部时，设D（x，-2x+6），分别根据△ADE≌△DPF，得出AE=DF，据此列出方程进行求解即可．
（1）证明：如图1，
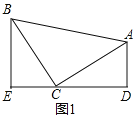
∵△ABC为等腰直角三角形，
∴CB=CA，∠ACD+∠BCE=90°，
又∵AD⊥ED，BE⊥ED，
∴∠D=∠E=90°，∠EBC+∠BCE=90°，
∴∠ACD=∠EBC，
在△ACD与△CBE中，
，
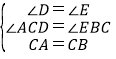∴△ACD≌△CBE（AAS）；
（2）①如图2，过点B作BC⊥AB，交l2于C，过C作CD⊥y轴于D，
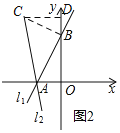
∵∠BAC=45°，
∴△ABC为等腰直角三角形，
由（1）可知：△CBD≌△BAO，
∴BD=AO，CD=OB，
∵直线l1：y=
x+4中，若y=0，则x=-3；若x=0，则y=4，
∴A（-3，0），B（0，4），
∴BD=AO=3，CD=OB=4，
∴OD=4+3=7，
∴C（-4，7），
设l2的解析式为y=kx+b，则
，
解得
，
∴l2的解析式：y=-7x-21；
②D（4，-2），（，）．
理由：当点D是直线y=-2x+6上的动点且在第四象限时，分两种情况：
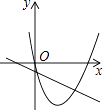
当点D在矩形AOCB的内部时，如图，过D作x轴的平行线EF，交直线OA于E，交直线BC于F，
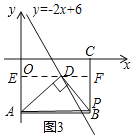
设D（x，-2x+6），则OE=2x-6，AE=6-（2x-6）=12-2x，DF=EF-DE=8-x，
由（1）可得，△ADE≌△DPF，则DF=AE，
即：12-2x=8-x，
解得x=4，
∴-2x+6=-2，
∴D（4，-2），
此时，PF=ED=4，CP=6=CB，符合题意；
当点D在矩形AOCB的外部时，如图，过D作x轴的平行线EF，交直线OA于E，交直线BC于F，
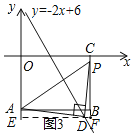
设D（x，-2x+6），则OE=2x-6，AE=OE-OA=2x-6-6=2x-12，DF=EF-DE=8-x，
同理可得：△ADE≌△DPF，则AE=DF，
即：2x-12=8-x，
解得x=，
∴-2x+6=-，
∴D（，-），
此时，ED=PF=，AE=BF=，BP=PF-BF=
＜6，符合题意．
