题目内容
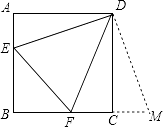
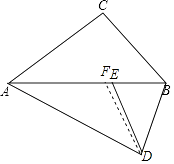
【题目】如图，已知△ABC，将△ABC绕点A顺时针旋转，使点C落在边AB上的点E处，点B落在点D处，连接BD，如果∠DAC=∠DBA，那么 
的值是 ． 
【答案】
【解析】解：如图，由旋转的性质得到AB=AD，∠CAB=∠DAB， ∴∠ABD=∠ADB，
∵∠CAD=∠ABD，
∴∠ABD=∠ADB=2∠BAD，
∵∠ABD+∠ADB+∠BAD=180°，
∴∠ABD=∠ADB=72°，∠BAD=36°，
过D作∠ADB的平分线DF，
∴∠ADF=∠BDF=∠FAD=36°，
∴∠BFD=72°，∴AF=DF=BD，
∴△ABD∽△DBF，
∴ 
，即 
，
解得 
= ，
故答案为： ．
由旋转的性质得到AB=AD，∠CAB=∠DAB，根据三角形的内角和得到∠ABD=∠ADB=72°，∠BAD=36°，过D作∠ADB的平分线DF推出△ABD∽△DBF，解方程即可得到结论．
练习册系列答案
相关题目
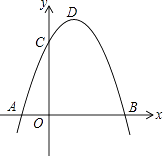
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A.抛物线于x轴的一个交点坐标为（﹣2，0）
B.抛物线与y轴的交点坐标为（0，6）
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的
