题目内容
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)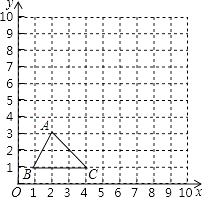
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1 , 请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2 , 请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.
【答案】
(1)解:如图所示:△A1B1C1,即为所求;
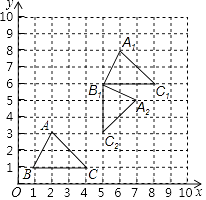
(2)解:如图所示:△A2B1C2,即为所求;

(3)解:线段B1C1变换到B1C2的过程中扫过区域的面积为: ![]() =
= ![]() π.
π.
【解析】(1)根据平移的性质得出对应点位置进而得出所求结论;
(2)根据旋转的性质得到对应点坐标,即可得出答案;
(3)先求出圆心角以及半径,再利用扇形面积公式直接计算得出结论.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2),以及对坐标与图形变化-平移的理解,了解新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目