题目内容
【题目】如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( ) 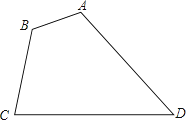
A.0<AD<7
B.2<AD<7
C.0<AD<13
D.1<AD<13
【答案】D
【解析】解答:连接AC.∵AB=2,BC=4,在△ABC中,根据三角形的三边关系,4-2<AC<2+4,即2<AC<6. ∴-6<-AC<-2,1<CD-AC<5,9<CD+AC<13,
在△ACD中,根据三角形的三边关系,得CD-AC<AD<CD+AC,
∴1<AD<13. 
分析:本题综合考查了三角形的三边关系.连接AC,求出AC的取值范围是解题关键.
【考点精析】根据题目的已知条件,利用三角形三边关系的相关知识可以得到问题的答案,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.

练习册系列答案
相关题目