Question

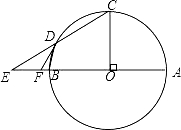
【题目】如图，AB为⊙O的直径，CO⊥AB于点O，D在⊙O上，连接BD、CD，延长CD与AB的延长线交于E，F在BE上，且FD=FE．

（1）求证：FD是⊙O的切线；

（2）若AF=10，tan∠BDF=，求EF的长．

Answer 1

【答案】(1)、证明过程见解析；(2)、2.5

【解析】

试题分析：(1)、连结OD，如图，由CO⊥AB得∠E+∠C=90°，根据等腰三角形的性质由FE=FD，OD=OC得到∠E=∠FDE，∠C=∠ODC，于是有∠FDE+∠ODC=90°，则可根据切线的判定定理得到FD是⊙O的切线；(2)、连结AD，如图，利用圆周角定理，由AB为⊙O的直径得到∠ADB=90°，则∠A+∠ABD=90°，加上∠OBD=∠ODB，∠BDF+∠ODB=90°，则∠A=∠BDF，易得△FBD∽△FDA，根据相似的性质得=，再在Rt△ABD中，根据正切的定义得到tan∠A=tan∠BDF==，于是可计算出DF=2.5，从而得到EF=2.5．

试题解析：(1)、连结OD，如图， ∵CO⊥AB， ∴∠E+∠C=90°， ∵FE=FD，OD=OC，

∴∠E=∠FDE，∠C=∠ODC， ∴∠FDE+∠ODC=90°， ∴∠ODF=90°， ∴OD⊥DF， ∴FD是⊙O的切线；

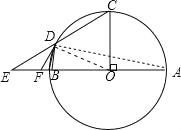
(2)、连结AD，如图， ∵AB为⊙O的直径， ∴∠ADB=90°， ∴∠A+∠ABD=90°， ∵OB=OD，

∴∠OBD=∠ODB， ∴∠A+∠ODB=90°， ∵∠BDF+∠ODB=90°， ∴∠A=∠BDF， 而∠DFB=∠AFD，

∴△FBD∽△FDA， ∴=， 在Rt△ABD中，tan∠A=tan∠BDF==， ∴=，

∴DF=2.5， ∴EF=2.5．