题目内容
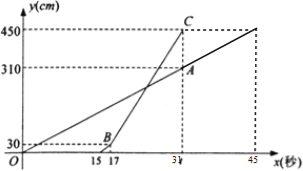
【题目】甲乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.两机器人行走的路程y(cm)与时间x(s)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)乙比甲晚出发_________秒,乙提速前的速度是每秒_________cm, ![]() =_________;
=_________;
(2)已知甲匀速走完了全程,请补全甲的图象;
(3)当x为何值时,乙追上了甲?

【答案】(1)15秒,30cm/s,31s;(2)见解析;(3)当x为24秒时,乙追上了甲.
【解析】试题分析:(1)根据图象x=15时,y=0知乙比甲晚15s;由x=17时y=30,求得提速前速度;根据时间=路程÷速度可求提速后所用时间,即可得到t值;
(2)甲的速度不变,可知只需延长OA到y=450即可;
(3)乙追上甲即行走路程y相等,求图象上OA与BC相交时x的值.
解:(1)由题意可知,当x=15时,y=0,故乙比甲晚出发15秒;
当x=15时,y=0;当x=17时,y=30;故乙提速前的速度是![]() (cm/s);
(cm/s);
∵乙出发一段时间后速度提高为原来的2倍,
∴乙提速后速度为30cm/s,
故提速后乙行走所用时间为:![]() (s),
(s),
∴t=17+14=31(s);
(2)由图象可知,甲的速度为:310÷31=10(cm/s),
∴甲行走完全程450cm需![]() (s),函数图象如下:
(s),函数图象如下:
(3)设OA段对应的函数关系式为y=kx,
∵A(31,310)在OA上,
∴31k=310,解得k=10,
∴y=10x.
设BC段对应的函数关系式为y=k1x+b,
∵B(17,30)、C(31,450)在BC上,
∴![]() ,解得
,解得![]() ,
,
∴y=30x﹣480,
由乙追上了甲,得10x=30x﹣480,解得x=24.
答:当x为24秒时,乙追上了甲.
故答案为:(1)15,15,31.