题目内容
【题目】已知:ABCD是平行四边形,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.
求证:AF=EC.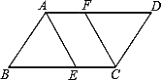
【答案】∵四边形ABCD是平行四边形,∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,∵AE平分∠BAD,CF平分∠BCD,∴∠EAB= ![]() ∠BAD,∠FCD=
∠BAD,∠FCD= ![]() ∠BCD,∴∠EAB=∠FCD,在△ABE和△CDF中
∠BCD,∴∠EAB=∠FCD,在△ABE和△CDF中 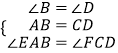 ∴△ABE≌△CDF,∴BE=DF.∵AD=BC∴AF=EC.
∴△ABE≌△CDF,∴BE=DF.∵AD=BC∴AF=EC.
【解析】根据平行四边形的性质得出相等的角和相等的线段,再利用角平分线的定义得出相等的角,利用ASA得出三角形全等,利用三角形全等的性质得出结论.
【考点精析】利用平行四边形的性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目