题目内容
如图所示,Rt△ABC中,∠C=90°,AB=4,△ABC的面积为
,则tanA+tanB等于( )
| 5 |
| 2 |

A、
| ||
B、
| ||
| C、4 | ||
D、
|
分析:设AC=x,BC=y,根据三角形面积可求出xy的值,然后根据勾股定理即可求出x2+y2=16,从而即可得出答案.
解答:解:设AC=x,BC=y,则
×xy=
,∴xy=5,
∵∠C=90°,AB=4,∴x2+y2=16,
∴tanA+tanB=
+
=
=
,
故选D.
| 1 |
| 2 |
| 5 |
| 2 |
∵∠C=90°,AB=4,∴x2+y2=16,
∴tanA+tanB=
| y |
| x |
| x |
| y |
| x2+y2 |
| xy |
| 16 |
| 5 |
故选D.
点评:本题考查了解直角三角形,属于基础题,关键是掌握勾股定理的运用.

练习册系列答案
相关题目
 6、如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为( )
6、如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为( ) 9、如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中一定相等的线段错误的有( )
9、如图所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中一定相等的线段错误的有( ) 如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.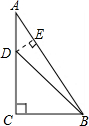 已知:如图所示,Rt△ABC中,∠C=90°,∠ABC=60°,DC=11,D点到AB的距离为2,求BD的长.
已知:如图所示,Rt△ABC中,∠C=90°,∠ABC=60°,DC=11,D点到AB的距离为2,求BD的长.