Question

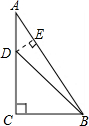已知：如图所示，Rt△ABC中，∠C=90°，∠ABC=60°，DC=11，D点到AB的距离为2，求BD的长．

Answer 1

分析：根据DE求AD的长度，根据AC=AD+CD即可求AC的长度，∵∠A=30°，∴AE=

3

DE=2

3

，且根据AB=2BC，AB²-BC²=AC²即可求得AB的长度，∴BE=AB-AE，根据BD=

DE2+BE2

即可求BD的长．

解答：解：DE⊥AB于E，且DE=2，
在Rt△ABC中，
∵∠ABC=60°，
∴∠A=30°．
在Rt△ADE中，
∵DE=2，
∴AD=4，AE=2

3

，
∵DC=11，∴AC=11+4=15，
∴AB=

15

3

×2=

30

3

=10

3

∴EB=AB-AE=8

3

，
在Rt△DEB中，DB2=DE2+EB2=22+(8

3

)2=4+192=196，
∴BD=14．
答：BD的长为14．

点评：本题考查了勾股定理的运用，考查了30°角在直角三角形中的运用，本题中巧妙地利用∠A=30°是解题的关键．