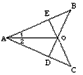
题目内容
已知:如图,在△ABC中,∠B=90度.O是BA上一点,以O为圆心、OB为半径的圆与AB交于点E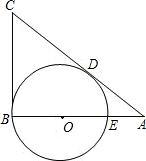 ,与AC切于点D,AD=2,AE=1.设P是线段BA上的动点(P与A、B不重合),BP=x.
,与AC切于点D,AD=2,AE=1.设P是线段BA上的动点(P与A、B不重合),BP=x.(1)求BE的长;
(2)求x为何值时,以P、A、D为顶点的三角形是等腰三角形;
(3)在点P的运动过程中,PD与△PBC的外接圆能否相切?若能,请证明;若不能,请说明理由;
(4)请再提出一个与动点P有关的数学问题,并直接写出答案.
分析:(1)由于AC切⊙O于点D,可根据切割线定理求得AB的长,即可得到BE的长;
(2)此题要分三种情况讨论:
①以A为顶角顶点,那么AP1=AD=2,根据AB的长即可求得此时BP1的长,即x的值;
②以P为顶角顶点,可作线段AD的中垂线,交AD于F、交AB于P2,则AF=FD、AP2=DP2;连接OD,易证得OD∥P2F,则P2F是△AOD的中位线,由此可得AP2=
OA,即可得到BP即x的值;
③以D为顶角顶点,此时AD=DP3,可过D作AB的垂线,设垂足为M,根据等腰三角形三线合一的性质,可得AM=MP3=
AP3,在Rt△ABC中,由切线长定理知BC=CD,已知AD、AB的长,即可由勾股定理求得BC、CD的长,易证得DM∥BC,根据平行线分线段成比例定理即可求得AM的长,由此可得到AP3的长,即可求得BP3即x的值.
(3)由于△PBC是直角三角形,则PC是△PBC外接圆的直径,若PD能与△PBC的外接圆相切,则PD⊥PC,在Rt△PBC和Rt△PCD中,分别用勾股定理表示出PC的平方:
BC2+BP2=CD2-PD2,在(2)题已证得BC=CD,则BP2=-PD2,即B、P、D三点重合,显然这种情况是不成立的,故PD不能与△PBC的外接圆相切.
(4)此题是开放性试题,可根据日常学习过程中的积累,来提出符合题意的问题.
(2)此题要分三种情况讨论:
①以A为顶角顶点,那么AP1=AD=2,根据AB的长即可求得此时BP1的长,即x的值;
②以P为顶角顶点,可作线段AD的中垂线,交AD于F、交AB于P2,则AF=FD、AP2=DP2;连接OD,易证得OD∥P2F,则P2F是△AOD的中位线,由此可得AP2=
| 1 |
| 2 |
③以D为顶角顶点,此时AD=DP3,可过D作AB的垂线,设垂足为M,根据等腰三角形三线合一的性质,可得AM=MP3=
| 1 |
| 2 |
(3)由于△PBC是直角三角形,则PC是△PBC外接圆的直径,若PD能与△PBC的外接圆相切,则PD⊥PC,在Rt△PBC和Rt△PCD中,分别用勾股定理表示出PC的平方:
BC2+BP2=CD2-PD2,在(2)题已证得BC=CD,则BP2=-PD2,即B、P、D三点重合,显然这种情况是不成立的,故PD不能与△PBC的外接圆相切.
(4)此题是开放性试题,可根据日常学习过程中的积累,来提出符合题意的问题.
解答: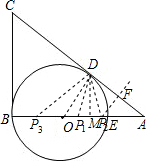 解:(1)∵AD与⊙O相切于点D,
解:(1)∵AD与⊙O相切于点D,
∴AD2=AE•AB;
由AD=2,AE=1,得AB=4;
∴BE=AB-AE=3;
(2)①以A为顶角顶点时,AP1=AD=2,x=BP1=BA-P1A=2;
②以P为顶角顶点时,作AD的垂直平分线P2F交AB于P2;
连接OD,则OD⊥AD,且OD∥P2F;
∴P2A=
OA=
x=BA-P2A=
;
③以D为顶角顶点时,DP3=DA=2,过D作DM⊥AB于M,则DM∥BC;
由BC2+AB2=(AD+DC)2,得BC=DC=3,AM=
,AP3=2AM=
,
∴x=BA-P3A=2AM=
,
综上所述,当x等于2、
、
时,△APD是等腰三角形;
(3)PD与△PBC的外接圆不能相切;
理由:假设PD与△PBC的外接圆相切,
则PD⊥PC,
在Rt△PBC中,PC>BC(直角三角形中,斜边大于直角边)
在Rt△PCD中,CD>PC(直角三角形中,斜边大于直角边)
而BC=CD,与上面的矛盾,所以,不存在.
(4)答案不唯一,如:
①x为何值时,以P、D、A为顶点的三角形与△ABC相似;
答:当x=
或
时,以P、D、A为顶点的三角形与△ABC相似.
②当x为何值时,PD+PC的和最小;
答:当x=
时,PD+PC的和最小.
 解:(1)∵AD与⊙O相切于点D,
解:(1)∵AD与⊙O相切于点D,∴AD2=AE•AB;
由AD=2,AE=1,得AB=4;
∴BE=AB-AE=3;
(2)①以A为顶角顶点时,AP1=AD=2,x=BP1=BA-P1A=2;
②以P为顶角顶点时,作AD的垂直平分线P2F交AB于P2;
连接OD,则OD⊥AD,且OD∥P2F;
∴P2A=
| 1 |
| 2 |
| 5 |
| 4 |
| 11 |
| 4 |
③以D为顶角顶点时,DP3=DA=2,过D作DM⊥AB于M,则DM∥BC;
由BC2+AB2=(AD+DC)2,得BC=DC=3,AM=
| 8 |
| 5 |
| 16 |
| 5 |
∴x=BA-P3A=2AM=
| 4 |
| 5 |
综上所述,当x等于2、
| 11 |
| 4 |
| 4 |
| 5 |
(3)PD与△PBC的外接圆不能相切;
理由:假设PD与△PBC的外接圆相切,
则PD⊥PC,
在Rt△PBC中,PC>BC(直角三角形中,斜边大于直角边)
在Rt△PCD中,CD>PC(直角三角形中,斜边大于直角边)
而BC=CD,与上面的矛盾,所以,不存在.
(4)答案不唯一,如:
①x为何值时,以P、D、A为顶点的三角形与△ABC相似;
答:当x=
| 3 |
| 2 |
| 12 |
| 5 |
②当x为何值时,PD+PC的和最小;
答:当x=
| 12 |
| 7 |
点评:此题涉及的知识点较多,有:切线的判定和性质、切线长定理、勾股定理、平行线分线段成比例定理、等腰三角形的判定和性质等重要知识点;需注意的是(2)题中,等腰三角形的腰和底不确定,要分类讨论,以免漏解.

练习册系列答案
相关题目
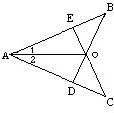 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,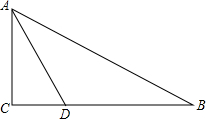 (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.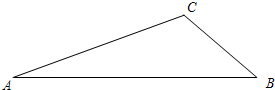 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.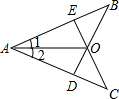 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,