题目内容
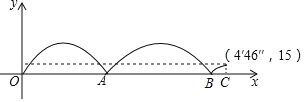
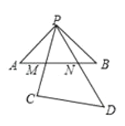
【题目】如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是( )
A.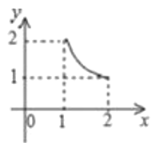 B.
B.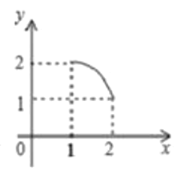 C.
C.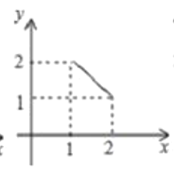 D.
D.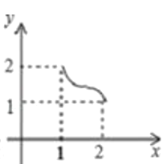
【答案】A
【解析】
试题作PH⊥AB于H,如图,
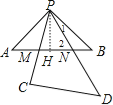
∵△PAB为等腰直角三角形,
∴∠A=∠B=45°,AH=BH=AB=1,
∴△PAH和△PBH都是等腰直角三角形,
∴PA=PB=![]() AH=
AH=![]() ,∠HPB=45°,
,∠HPB=45°,
∵∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N
而∠CPD=45°,
∴1≤AN≤2,即1≤x≤2,
∵∠2=∠1+∠B=∠1+45°,∠BPM=∠1+∠CPD=∠1+45°,
∴∠2=∠BPM,
而∠A=∠B,
∴△ANP∽△BPM,
∴![]() ,即
,即![]() ,
,
∴y=![]() ,
,
∴y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.
故选A.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目