题目内容
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,E为BD上的一点,连接EA,将EA绕点E逆时针旋转90°得线段EF,连接FB.

(1)如图a,点E在OB上,
①求∠FEB+∠BAE的度数;
②求证:ED﹣EB=![]() BF;
BF;
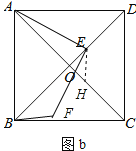
(2)如图b,当E在OD上时,按已知条件补全图形,直接写出ED、EB、BF三条线段的数量关系.
【答案】(1)①45°;②见解析;(2)EB﹣ED=![]() BF.
BF.
【解析】
试题分析:(1)①根据已知条件易证得∠BAE=∠F,根据三角形外角的性质得出∠F+∠FEB=∠OBC=45°,即可求得∠FEB+∠BAE=45°;②在OA上截取OH=OE,连接EH,四边形ABCD是正方形,求得∠OHE=∠OEH=45°,由∠AEF=90°,得出∠FEB+∠AEH=45°,即可求得AEH=∠F,根据∠FEB+∠AEO=90°,∠AEO+∠EAH=90°得到∠FEB=∠EAH,然后根据ASA证得△FEB≌△EAH,得出BF=EH,根据等腰直角三角形的性质求得![]() =
=![]() 得出OE=
得出OE=![]() BF,因为ED﹣EB=OD+OE﹣(OB﹣OE)=2OE,即可证得ED﹣EB=
BF,因为ED﹣EB=OD+OE﹣(OB﹣OE)=2OE,即可证得ED﹣EB=![]() BF;
BF;
(2)在OC上截取OH=OE,连接EH,得出AH=BE,根据AC⊥BD,∠AEF=90°,得出∠EAH=∠FEB,根据SAS证得△FEB≌△EAH,得出BF=EH,根据等腰直角三角形的性质求得![]() =
=![]() 得出OE=
得出OE=![]() BF,因为EB﹣ED=2OE,即可证得EB﹣ED=
BF,因为EB﹣ED=2OE,即可证得EB﹣ED=![]() BF.
BF.
解:(1)①如图a,∵∠AEF=90°,∠ABF=90°,∠1=∠2,
∴∠BAE=∠F,
∵∠F+∠FEB=∠OBC=45°
∴∠FEB+∠BAE=45°;
②在OA上截取OH=OE,连接EH,
∵四边形ABCD是正方形,
∴∠AOB=90°,
∴∠OHE=∠OEH=45°,
∵∠AEF=90°,
∴∠FEB+∠AEH=45°,
∴∠AEH=∠F,
∵∠AEF=90°,
∴∠FEB+∠AEO=90°,
∵∠AEO+∠EAH=90°,
∴∠FEB=∠EAH,
在△FEB和△EAH中,
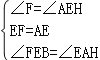 ,
,
∴△FEB≌△EAH(ASA),
∴BF=EH,
在等腰直角三角形EOH中,![]() =
=![]()
∴OE=![]() BF,
BF,
∵ED﹣EB=OD+OE﹣(OB﹣OE)=2OE,
∴ED﹣EB=![]() BF;
BF;
(2)ED、EB、BF三条线段的数量关系为:EB﹣ED=![]() BF,
BF,
在OC上截取OH=OE,连接EH,
∵四边形ABCD是正方形,
∴OA=OB,
∴OA+OH=OB+OE,即AH=BE,
∵AC⊥BD,∠AEF=90°,
∴∠EAH=∠FEB,
在△FEB和△EAH中,
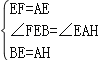 ,
,
∴△FEB≌△EAH(SAS),
∴BF=EH,
在等腰直角三角形EOH中,![]() =
=![]()
∴OE=![]() BF,
BF,
∵BE﹣DE=2OE,
∴EB﹣ED=![]() BF.
BF.