题目内容
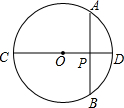（1997•河南）如图，O是圆心，OP⊥AB，AP=4厘米，PD=2厘米，那么OP=3
3
厘米．分析：连接OA，设OA=r，则OP=OD-PD=r-2，在Rt△AOP中，利用勾股定理求出r的值，进而可得出结论．
解答：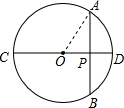
解：连接OA，设OA=r，则OP=OD-PD=r-2，
在Rt△AOP中，
∵OA2=OP2+AP2，即r2=（r-2）2+42，解得r=5cm，
∴OP=r-2=5-2=3cm．
故答案为：3．
解：连接OA，设OA=r，则OP=OD-PD=r-2，在Rt△AOP中，
∵OA2=OP2+AP2，即r2=（r-2）2+42，解得r=5cm，
∴OP=r-2=5-2=3cm．
故答案为：3．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．
练习册系列答案
相关题目
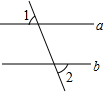（1997•河南）如图，直线a∥b，直线c与a、b都相交，且∠1=80°，那么∠2=
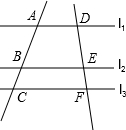（1997•河南）如图，l1∥l2∥l3，BC=3，
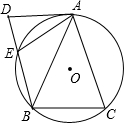（1997•河南）如图，△ABC内接于⊙O，AB=AC，AD是⊙O的切线，BD∥AC，BD交⊙O于点E，连接AE．求证：AE2=DE•DB．
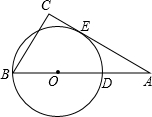（1997•河南）如图，a、b、c分别是△ABC中∠A、∠B、∠C的对边，且a、b是关于x的一元二次方程x2+4（c+2）=（c+4）x的两个根．点D在AB上，以BD为直径的⊙O切AC于点E．