题目内容
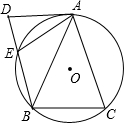 (1997•河南)如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE.求证:AE2=DE•DB.
(1997•河南)如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE.求证:AE2=DE•DB.分析:先证∠DAE=∠BAC,∠DEA=∠C,推出△DAE∽△BAC,推出AD=AE,根据切割线定理得出AD2=DE•BD,即可得出答案.
解答:证明:∵AD是⊙O的切线,
∴∠DAE=∠ABD,
∵BD∥AC,
∴∠CAB=∠ABD,
∴∠DAE=∠CAB,
∵四边形AEBC内接于⊙O,
∴∠AED=∠ACB.
∴△ADE∽△ABC,
∴
=
,
由AB=AC,得
AD=AE,
根据切割线定理,得
AE2=AD2=DE•DB.

∴∠DAE=∠ABD,
∵BD∥AC,
∴∠CAB=∠ABD,
∴∠DAE=∠CAB,
∵四边形AEBC内接于⊙O,
∴∠AED=∠ACB.
∴△ADE∽△ABC,
∴
| AD |
| AB |
| AE |
| AC |
由AB=AC,得
AD=AE,
根据切割线定理,得
AE2=AD2=DE•DB.
点评:本题考查了切线的性质,圆内接四边形的性质,等腰三角形的性质,平行线的性质,相似三角形的性质和判定等知识点的综合运用,主要考查学生综合运用知识进行推理的能力.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
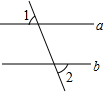 (1997•河南)如图,直线a∥b,直线c与a、b都相交,且∠1=80°,那么∠2=
(1997•河南)如图,直线a∥b,直线c与a、b都相交,且∠1=80°,那么∠2=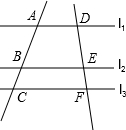 (1997•河南)如图,l1∥l2∥l3,BC=3,
(1997•河南)如图,l1∥l2∥l3,BC=3,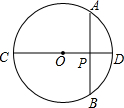 (1997•河南)如图,O是圆心,OP⊥AB,AP=4厘米,PD=2厘米,那么OP=
(1997•河南)如图,O是圆心,OP⊥AB,AP=4厘米,PD=2厘米,那么OP=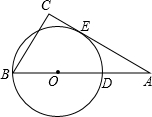 (1997•河南)如图,a、b、c分别是△ABC中∠A、∠B、∠C的对边,且a、b是关于x的一元二次方程x2+4(c+2)=(c+4)x的两个根.点D在AB上,以BD为直径的⊙O切AC于点E.
(1997•河南)如图,a、b、c分别是△ABC中∠A、∠B、∠C的对边,且a、b是关于x的一元二次方程x2+4(c+2)=(c+4)x的两个根.点D在AB上,以BD为直径的⊙O切AC于点E.