题目内容
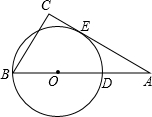（1997•河南）如图，a、b、c分别是△ABC中∠A、∠B、∠C的对边，且a、b是关于x的一元二次方程x2+4（c+2）=（c+4）x的两个根．点D在AB上，以BD为直径的⊙O切AC于点E．（1）判断△ABC的形状；
（2）若tanA=
| 3 | 4 |
分析：（1）由a、b是关于x的一元二次方程x2+4（c+2）=（c+4）x的两个根，根据根与系数的关系，可得a+b=c+4，ab=4（c+2），继而可得a2+b2=c2，则可判定△ABC是直角三角形．
（2）连接OE，由tanA=
与a+b=c+4，可求得a，b，c的值，又由平行线分线段成比例定理，可求得半径的长，继而求得答案．
（2）连接OE，由tanA=
| 3 |
| 4 |
解答：解：（1）△ABC是直角三角形．
理由：∵a、b是关于x的一元二次方程x2+4（c+2）=（c+4）x的两个根．
∴a+b=c+4，ab=4（c+2），（1分）
∴a2+b2=（a+b）2-2ab
=（c+4）2-8（c+2）
=c2．
∴△ABC是直角三角形．（2分）
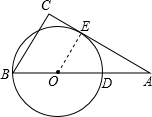（2）∵∠C=90°，
∴tanA=
=
，
设a=3k，则b=4k，从而c=5k（k＞0）．
∵a+b=c+4，
∴3k+4k=5k+4，
解得：k=2．
∴a=6，b=8，c=10．（5分）
连接OE．（6分）
∵AE是切线，
∴OE⊥AE．
又∵BC⊥AC，
∴OE∥BC．（7分）
∴△AOE∽△ABC，
∴
=
，
∴
=
，
解得：OE=
，
在Rt△AOE中，AE=
=
=5．
理由：∵a、b是关于x的一元二次方程x2+4（c+2）=（c+4）x的两个根．
∴a+b=c+4，ab=4（c+2），（1分）
∴a2+b2=（a+b）2-2ab
=（c+4）2-8（c+2）
=c2．
∴△ABC是直角三角形．（2分）
（2）∵∠C=90°，∴tanA=
| a |
| b |
| 3 |
| 4 |
设a=3k，则b=4k，从而c=5k（k＞0）．
∵a+b=c+4，
∴3k+4k=5k+4，
解得：k=2．
∴a=6，b=8，c=10．（5分）
连接OE．（6分）
∵AE是切线，
∴OE⊥AE．
又∵BC⊥AC，
∴OE∥BC．（7分）
∴△AOE∽△ABC，
∴
| OE |
| BC |
| OA |
| AB |
∴
| OE |
| 6 |
| 10-OE |
| 10 |
解得：OE=
| 15 |
| 4 |
在Rt△AOE中，AE=
| OE |
| tanA |
| ||
|
点评：此题考查了切线的性质、相似三角形的判定与性质、勾股定理的逆定理、根与系数的关系以及三角函数等知识．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与方程思想的应用．
练习册系列答案
相关题目
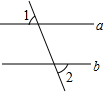（1997•河南）如图，直线a∥b，直线c与a、b都相交，且∠1=80°，那么∠2=
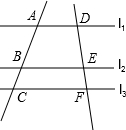（1997•河南）如图，l1∥l2∥l3，BC=3，
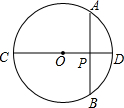（1997•河南）如图，O是圆心，OP⊥AB，AP=4厘米，PD=2厘米，那么OP=
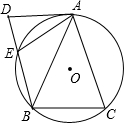（1997•河南）如图，△ABC内接于⊙O，AB=AC，AD是⊙O的切线，BD∥AC，BD交⊙O于点E，连接AE．求证：AE2=DE•DB．