题目内容
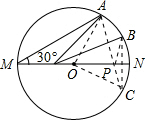
如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，B为AN弧的中点，P是直径MN上一动点，则PA+PB的最小值为______．
作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．
此时PA+PB最小，且等于AC的长．
连接OA，OC，根据题意得：
∵∠AMN=30°，
∴弧AN的度数是60°，
∵B为AN弧的中点，
∴弧BN的度数是30°，
∵NO⊥BC，
∴
=
，
∴弧CN的度数是30°，
∴
=
+
=90°
∴∠AOC=90°，
又∵OA=OC=1，
∴AC=
=
．
即PA+PB的最小值为：
，
故答案为：
．
此时PA+PB最小，且等于AC的长．
连接OA，OC，根据题意得：
∵∠AMN=30°，
∴弧AN的度数是60°，
∵B为AN弧的中点，
∴弧BN的度数是30°，
∵NO⊥BC，
∴
 |
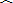| BN |
|
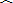| CN |
∴弧CN的度数是30°，
∴
|
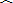| AC |
|
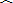| AN |
|
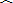| CN |
∴∠AOC=90°，
又∵OA=OC=1，
∴AC=
| 12+12 |
| 2 |
即PA+PB的最小值为：
| 2 |
故答案为：
| 2 |
练习册系列答案
名题金卷系列答案
相关题目
