题目内容
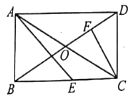
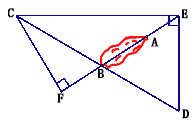
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
【答案】(1) 16.7(海里).(2) ![]() .
.
【解析】
试题分析:(1)在Rt△CED中,利用三角函数求出CE,CD的长,根据中点的定义求得BE的长,AB=BE-AE即可求解;
(2)设BF=x海里.在Rt△CFB中,利用勾股定理求得CF2=CB2-BF2=252-x2=625-x2.在Rt△CFE中,列出关于x的方程,求得x的值,从而求得sin∠BCF的值.
(1)在Rt△CED中,∠CED=90°,DE=30海里,
∴cos∠D=![]() ,
,
∴CE=40(海里),CD=50(海里).
∵B点是CD的中点,
∴BE=![]() CD=25(海里)
CD=25(海里)
∴AB=BE-AE=25-8.3=16.7(海里).
答:小岛两端A、B的距离为16.7海里.
(2)设BF=x海里.
在Rt△CFB中,∠CFB=90°,
∴CF2=CB2-BF2=252-x2=625-x2.
在Rt△CFE中,∠CFE=90°,
∴CF2+EF2=CE2,即625-x2+(25+x)2=1600.
解得x=7.
∴sin∠BCF=![]() .
.
考点: 解直角三角形的应用.

练习册系列答案
相关题目