题目内容
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
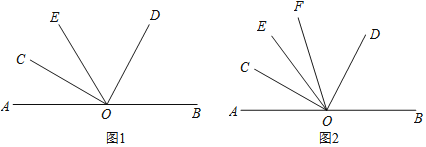
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
【答案】(1)见解析;(2)∠AOE=67.5°
【解析】
(1)根据角的和差定义证明即可.
(2)设∠EOF=x,构建方程求出x即可解决问题.
(1)证明:∵OE是∠AOD的平分线,
∴∠AOD=2∠EOD,
∴∠BOD=180°﹣∠AOD
=180°﹣2∠DOE
=2(90°﹣∠DOE)=2∠COE.
(2)解:设∠EOF=x,则∠EOC=3x,
∴∠COF=∠EOC+∠EOF=4x,
∵OF平分∠COD,∠COD=90°,
∴∠COF=45°,即4x=45°,
∴x=11.25°,
∵OC平分∠AOE,
∴∠AOE=2∠AOC=6x=67.5°.

练习册系列答案
相关题目