题目内容
已知四边形ABCD的对角线AC与BD相交于点O，若S△AOB=4，S△COD=9，则四边形ABCD的面积S四边形ABCD的最小值为（ ）A．21
B．25
C．26
D．36
【答案】分析：分别表示出△AOD、△BOC的面积，即可得到四边形ABCD的面积表达式，然后利用换元法结合不等式的性质来求得四边形ABCD的最小面积．
解答：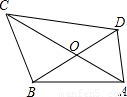
解：设点A到边BD的距离为h．
如图，任意四边形ABCD中，S△AOB=4，S△COD=9；
∵S△AOD=
OD•h，S△AOB=
OB•h=4，
∴S△AOD=OD•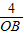
=4×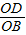
，S△BOC=OB•
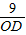=9×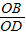
；
设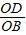
=x，则S△AOD=4x，S△BOC=
；
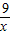∴S四边形ABCD=4x+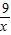
+13≥2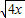
•
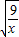+13=12+13=25；
故四边形ABCD的最小面积为25．
故选B．
点评：此题主要考查了三角形面积的求法、不等式的性质等知识，需要识记的内容有：
不等式的性质：a2+b2-2ab=（a-b）2≥0，即a2+b2≥2ab．（即算术平均数与几何平均数的关系）
解答：
解：设点A到边BD的距离为h．如图，任意四边形ABCD中，S△AOB=4，S△COD=9；
∵S△AOD=
OD•h，S△AOB=OB•h=4，∴S△AOD=OD•
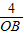=4×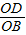，S△BOC=OB•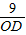=9×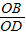；设
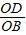=x，则S△AOD=4x，S△BOC=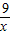；∴S四边形ABCD=4x+
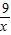+13≥2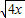•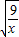+13=12+13=25；故四边形ABCD的最小面积为25．
故选B．
点评：此题主要考查了三角形面积的求法、不等式的性质等知识，需要识记的内容有：
不等式的性质：a2+b2-2ab=（a-b）2≥0，即a2+b2≥2ab．（即算术平均数与几何平均数的关系）
练习册系列答案
互动英语系列答案
相关题目
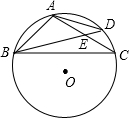如图，已知四边形ABCD的外接圆⊙O的半径为2，对角线AC与BD的交点为E，AE=EC，AB=
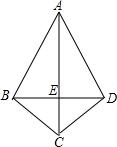如图，△ABC与△ADC关于直线AC对称，连接BD，若已知四边形ABCD的面积是125，AC=25，则BD的长为
如图，已知四边形ABCD的对角线互相垂直，若适当添加一个条件，就能判定该四边形是菱形．那么这个条件可以是（ ）
如图，已知四边形ABCD的四个顶点的坐标分别为A（0，0），B（9，0），C（7，5），D（2，7），将该四边形各顶点的横坐标都增加2，纵坐标都增加3，其面积为（ ）