题目内容
【题目】如图所示,在平面直角坐标系xOy中,B , C两点的坐标分别为 ![]() ,
, ![]() ,CD⊥y轴于点D , 直线l 经过点D.
,CD⊥y轴于点D , 直线l 经过点D.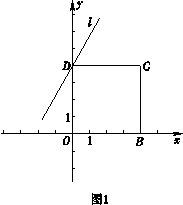
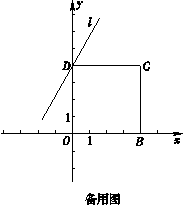
(1)直接写出点D的坐标;
(2)作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.
①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ![]() ,从而证明结论.
,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
【答案】
(1)
解: ![]()
(2)
解:①补全图形见图7.
②BF⊥直线l.
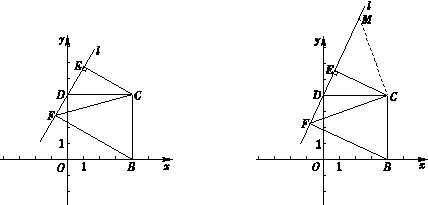
③法1:
证明:如图8,作CM⊥CF,交直线l于点M.
∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵ CE⊥直线l,CM⊥CF, ![]() ,
,
可得△CEF,△CEM 为等腰直角三角形, ![]() ,
,
CF=CM ①
∵ ![]() ,
, ![]() ,
,
∴ ∠BCF=∠DCM ②
又∵CB=CD, ③
∴ △CBF≌△CDM.
∴ ![]()
∴ ![]() .
.
∴ BF⊥直线l.
法2:
证明:如图9,作BN⊥CE,交直线CE于点N.
∵ ![]() ,
, ![]() ,
, ![]() ,
,

∴ ![]() ,
, ![]() .
.
∵ CE⊥直线l, BN⊥CE,
∴ ∠BNC=∠CED=90° ①
∴ ![]() ,
, ![]() .
.
∴ ∠1=∠2 . ②
又∵CB=CD, ③
∴ △BCN≌△CDE.
∴ BN= CE.
又∵ ![]() ,
,
可得△CEF为等腰直角三角形,EF = CE.
∴ BN= EF.
又∵ ![]() ,
,
∴ BN∥FE.
∴ 四边形BFEN为平行四边形.
又∵ ![]() ,
,
∴ 平行四边形BFEN为矩形.
∴ ![]() .
.
∴ BF⊥直线l
【解析】(1)由图可以直接得出D点坐标.
(2)③法1:如图8,作CM⊥CF , 交直线l于点M .
由 B(4,0) , C(4,4) , D(0,4) ,可得△CEF,△CEM 为等腰直角三角形, 由等腰三角形性质和已知条件证△CBF≌△CDM.由全等三角形的性质
BF⊥直线l.
【考点精析】利用等腰直角三角形和余角和补角的特征对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;互余、互补是指两个角的数量关系,与两个角的位置无关.

 阅读快车系列答案
阅读快车系列答案