题目内容
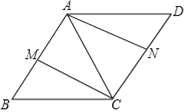
【题目】如图，在ABCD中，AC=BC，M、N分别是AB和CD的中点．
（1）求证：四边形AMCN是矩形；
（2）若∠B=60°，BC=4，求ABCD的面积．
【答案】（1）见解析；（2）8
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，由已知条件得出AM
CN，AM=CN，证出四边形AMCN是平行四边形，由等腰三角形的性质得出
即可得出四边形AMCN是矩形．
平行四边形的面积=底
高即可求出.
试题解析：（1）证明：∵四边形ABCD是平行四边形，
∴AB
CD，AB=CD，
∵M、N分别是AB和CD的中点，
∴AM=BM,AM
CN，AM=CN，
∴四边形AMCN是平行四边形，
又∵AC=BC，AM=BM，
∴CM⊥AB，
∴四边形AMCN是矩形.
（2）
中， 
∴ABCD的面积为
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
