Question

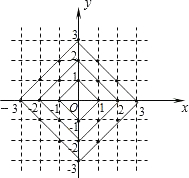在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上及其内部的整点个数共有（　　）个．

• A、40
• B、200
• C、221
• D、121

Answer 1

分析：找到从内到外每个正方形的整点的个数，找到n与第n个正方形整点的个数的规律，并根据其解决题目．

解答：解：第一个正方形及内部的整点个数为4+1=4×1+1，
第二个正方形及内部的整点个数为4×2+4×1+1，
第三个正方形及内部的整点个数为4×3+4×2+4×1+1，
故找到规律第n个正方形的整点个数4（1+2+3+…+n）+1
=4×

n(n+1)

2

+1
=2n（n+1）+1，
当n=10时，正方形及内部的整点数为20×（10+1）+1=221，
故选 C．

点评：本题考查了正方形各边相等的性质，本题中找到第n正方形及其内部的整点个数的规律并根据其求解是解题的关键．