题目内容
综合实践问题背景
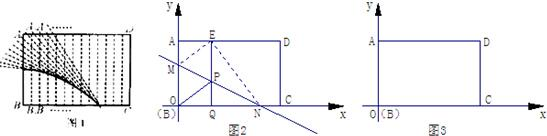
某课外兴趣小组在一次折纸活动中,折叠一张带有条格的长方形纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格所在直线的交点,用平滑的曲线顺次连接各交点,得到一条曲线.
探索
如图2,在平面直角坐标系xOy中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=m,AD=n(m≤n),将纸片折叠,MN是折痕,使点B落在边AD上的E处,过点E作EQ⊥BC,垂足为Q,交直线MN于点P,连接OP
(1)求证:四边形OMEP是菱形;
(2)设点P坐标为(x,y),求y与x之间的函数关系式,并写出自变量x的取值范围.(用含m、n的式子表示)
运用
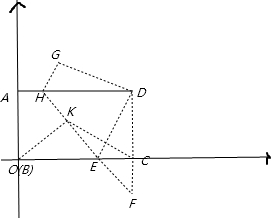
(3)将长方形纸片ABCD如图3所示放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在K,使得△KCF的面积是△KOC面积的
| 5 | 3 |
分析:(1)如果四边形的四边相等,那么这个四边形是菱形.
(2)根据P点的坐标,可表示出E点的坐标,从而可知道OP的长,用勾股定理表示出解析式.
(3)画出图形,从图上可看出不存在.
(2)根据P点的坐标,可表示出E点的坐标,从而可知道OP的长,用勾股定理表示出解析式.
(3)画出图形,从图上可看出不存在.
解答:解:(1)∵AB∥EQ,
∴∠OMP=∠EPM,
∵∠EPM=∠OPM,
∴∠OMP=∠OPM,
∴OM=OP,
∵OM=EM,OP=EP,
∴四边形OMEP是菱形.
(2)∵E点的坐标为(x,m),
OP=EP=m-y,
∴(m-y)2=x2+y2.
y=-
+
(0<x<
).
(3)根据(2)知,点K的坐标为(x,-
+4).
设EC的长为x,DE=BE=12-x,DC=8,
x2+82=(12-x)2
x=
.
同理:GH=
,DH=
,
△ECF∽△DHF,
∴
=
,
即
=
,
解得CF=5,
∴△ECF的面积为:
CE•CF=
×
×5=
.
△OCK的面积为:
×12(-
+4).
△KCF的面积:
×
(-
+4)+
.
根据△KCF的面积是△KOC面积得,
×
×12(-
+4)=
×
(-
+4)+
,
可求出x=4
,
所以K的坐标为:(4
,1).
∴∠OMP=∠EPM,
∵∠EPM=∠OPM,
∴∠OMP=∠OPM,
∴OM=OP,
∵OM=EM,OP=EP,
∴四边形OMEP是菱形.
(2)∵E点的坐标为(x,m),
OP=EP=m-y,
∴(m-y)2=x2+y2.
y=-
| x2 |
| 2m |
| m |
| 2 |
| m2+n2 |
| 2n |
(3)根据(2)知,点K的坐标为(x,-
| x2 |
| 16 |
设EC的长为x,DE=BE=12-x,DC=8,
x2+82=(12-x)2
x=
| 10 |
| 3 |
同理:GH=
| 10 |
| 3 |
| 26 |
| 3 |

△ECF∽△DHF,
∴
| EC |
| DH |
| CF |
| DF |
即
| ||
|
| CF |
| CF+8 |
解得CF=5,
∴△ECF的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 25 |
| 3 |
△OCK的面积为:
| 1 |
| 2 |
| x2 |
| 16 |
△KCF的面积:
| 1 |
| 2 |
| 10 |
| 3 |
| x2 |
| 16 |
| 25 |
| 3 |
根据△KCF的面积是△KOC面积得,
| 5 |
| 3 |
| 1 |
| 2 |
| x2 |
| 16 |
| 1 |
| 2 |
| 10 |
| 3 |
| x2 |
| 16 |
| 25 |
| 3 |
可求出x=4
| 3 |
所以K的坐标为:(4
| 3 |
点评:本题考查了菱形的判定定理,矩形的性质,相似三角形的性质,相似三角形的面积比等于相似比的平方以及翻折变换的知识.

练习册系列答案
相关题目

 ,若存在,写出点K的坐标;若不存在,请说明理由.
,若存在,写出点K的坐标;若不存在,请说明理由.
 ,若存在,写出点K的坐标;若不存在,请说明理由.
,若存在,写出点K的坐标;若不存在,请说明理由.