Question

（2013•山西模拟）问题背景  某课外学习小组在一次学习研讨中，得到如下命题：
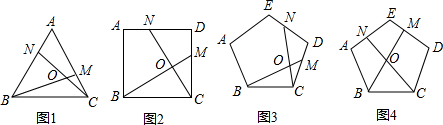
①如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN．
②如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
然后运用类比的思想提出了如下的命题：
③如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．

任务要求
（1）请你对命题③进行证明；
（2）请你继续完成下面的探索：如图4，在五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，当∠BON=108°时，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．

Answer 1

分析：（1）根据正五边形性质得出∠D=∠BCM=108°，BC=CD，求出∠CBM=∠DCN，根据ASA推出△BCM≌△CDN即可；
（2）连接CE，BD，根据正五边形性质得出∠AED=∠EDC=∠BCD=108°，ED=DC=BC，求出N、E、M、O四点共圆，求出∠ENC=∠BMD，证△BCD≌△CDE，推出BD=CE，∠DEC=∠BDC，求出∠NEC=∠MDB，根据AAS证△ECN≌△DBM，即可得出答案．

解答：（1）证明：∵五边形ABCDE是正五边形，
∴∠D=∠BCM=

(5-2)×180°

5

=108°，BC=CD，
∵∠BON=108°，
∴∠BON=∠CBM+∠BCN=108°，∠BCD=∠BCN+∠DCN=108°，
∴∠CBM=∠DCN，
在△BCM和△CDN中，

∠CBM=∠DCN BC=CD ∠BCM=∠D

，
∴△BCM≌△CDN（ASA），
∴BM=CN．

（2）BM=CN还成立，
理由是：连接CE，BD，
∵五边形ABCDE是正五边形，
∴∠AED=∠EDC=∠BCD=108°，ED=DC=BC，
∵∠BON=108°，
∴∠NOM+∠AED=180°，
∴N、E、M、O四点共圆，
∴∠ENC+∠EMB=180°，
∵∠EMB+∠DMB=180°，
∴∠ENC=∠BMD，
在△BCD和△CDE中，

BC=DE ∠BCD=∠CDE CD=CD

，
∴△BCD≌△CDE（SAS），
∴BD=CE，∠DEC=∠BDC，
∵∠EDC=∠AED=108°，
∴∠AED-∠DEC=∠CDE-∠CDB，
即∠NEC=∠MDB，
在△ECN和△DBM中，

∠ENC=∠DMB ∠NEC=∠MDB CE=BD

，
∴△ECN≌△DBM（AAS），
∴BM=CN，
即BM=CN还成立．

点评：本题考查了四点共圆，圆内接四边形的性质，全等三角形的性质和判定，正多边形的性质的应用，主要考查学生的推理能力．