题目内容
若一个正六边形的周长为24,则该正六边形的面积为 ▲ .

根据题意画出图形,如图,连接OB,OC,过O作OM⊥BC于M,
∴∠BOC=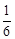 ×360°=60°。
×360°=60°。
∵OB=OC,∴△OBC是等边三角形。∴∠OBC=60°。
∵正六边形ABCDEF的周长为24,∴BC=24÷6=4。
∴OB=BC=4,∴BM=OB·sin∠OBC =4·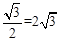 。
。
∴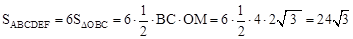 。
。

∴∠BOC=
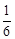 ×360°=60°。
×360°=60°。∵OB=OC,∴△OBC是等边三角形。∴∠OBC=60°。
∵正六边形ABCDEF的周长为24,∴BC=24÷6=4。
∴OB=BC=4,∴BM=OB·sin∠OBC =4·
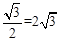 。
。∴
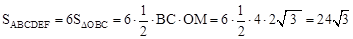 。
。
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
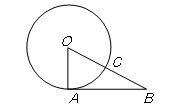
 B=30°,则劣弧
B=30°,则劣弧 的长是 .(结果保留
的长是 .(结果保留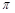 )
)
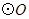 中,
中,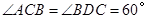 ,
, .
.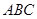 的度数;
的度数;
 的长为【 】
的长为【 】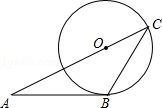
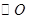 半径
半径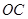 垂直于弦
垂直于弦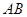 ,点
,点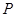 在
在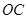 的延长线上,
的延长线上,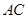 平分
平分 .
.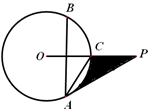
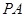 是
是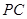 =
=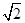 ,
,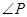 =30°,求阴影部分面积.(保留根号和
=30°,求阴影部分面积.(保留根号和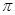 )
)