��Ŀ����
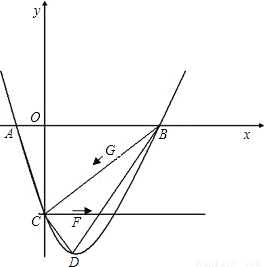
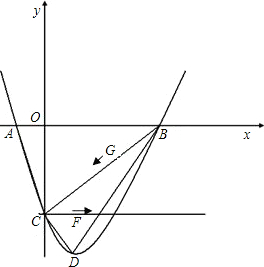
��֪��ͼ������y=x2-2x-3��x�ύ��A��B���㣨A��B����ࣩ��y�ύ��C�㣬����ΪD����1�����A��B��C��D�ĵ����ꣻ
��2���жϡ�AOC���BCD�Ƿ����ƣ���˵�����ɣ�
��3����C��ֱ��CEƽ��x�ύ��������һ������ΪE������F��C�㿪ʼ����ÿ��
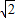 ����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�
����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���������1�������ߵĽ���ʽ�У���y=0������õ�A��B�����꣬��x=0������õ�C�����ꣻ�������ߵĽ���ʽ��Ϊ��������ʽ��������õ�D�����꣮
��2��������֪��A��B��C��D�����꣬��������������θ��Ե����߳���Ȼ��֤��BCD����AOC�Ķ�Ӧ�߳ɱ������ɣ�
��3������������������C��F��H��G�ĵ�Ϊ�����ƽ���ı��ε�H�����꣬Ȼ����������ߵĽ���ʽ�н�����֤���ɣ�
�ֱ��C��F��G��FG��CG��CF��ƽ���ߣ���ô��Щƽ���ߵĽ��㼴Ϊ�����H�㣬��ΪH1��H2��H3����G��GN��x����N�����ڡ�OBC=45°�����ɸ���BG�ij���ʾ��GN��BN��ֵ����CP�ij�����ã�����ƽ���ı��ε����ʣ�����Ա�ƽ������ȣ������ɵõ�H1��H2�����꣬Ȼ�����Ǵ��������ߵĽ���ʽ�н�����֤���ɣ������÷����н⣬�����õĽ⼴Ϊ����������H�����꣬���⣬����˵�������ڷ���������H�㣮H3��������ͬ�ϣ�
����⣺��1����y=0����x2-2x-3=0����x=3��x=-1��
��A��-1��0����B��3��0����
��x=0����y=-3��
��C��0��-3����
����y=x2-2x-3=��x-1��2-4��
�ʶ���D��1��-4����
��2�����ƣ��������£�
��A��-1��0����B��3��0����C��0��-3����D��1��-4����
��OA=1��OC=3��AC=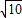 ��
��
CD=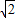 ��BC=3
��BC=3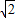 ��BD=2
��BD=2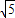 ��
��
��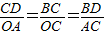 =
= ��
��
�ʡ�AOC�ס�DCB��
��3���ֱ��C��F��G��FG��CG��CF��ƽ���ߣ����߽���H1��H2��H3����ͼ����
���ı���CFGH1���ı���CFH2G���ı���H3FGC����ƽ���ı��Σ�
��G��GM��x����M��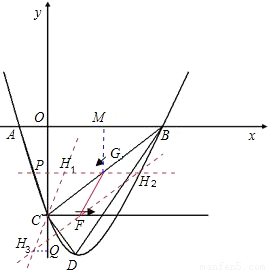
����OB=OC=3�����OBC=45°��
��֪BG=4t����BM=MG=2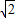 t��OM=3-2
t��OM=3-2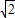 t��
t��
��G��3-2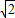 t��-2
t��-2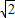 t����
t����
�����ı���CFGH1���ı���CFH2G����ƽ���ı��Σ�
��H1G=GH2=CF=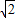 t��
t��
��H1��3-3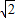 t��-2
t��-2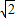 t����H2��3-
t����H2��3-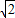 t��-2
t��-2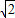 t����
t����
��H1���������ߵĽ���ʽ�еã�
��3-3 t��2-2��3-3
t��2-2��3-3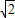 t��-3=-2
t��-3=-2 t��
t��
��9t2-5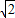 t=0��
t=0��
���t=0����ȥ����t=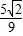 ��
��
��t= ʱ��H1��-
ʱ��H1��- ��-
��- ����
����
��H2���������ߵĽ���ʽ�еã�
��3-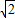 t��2-2��3-
t��2-2��3-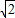 t��-3=-2
t��-3=-2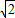 t��
t��
��t2-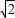 t=0��
t=0��
���t=0����ȥ����t=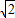 ��
��
��t=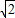 ʱ��H2��1��-4����
ʱ��H2��1��-4����
��G��GP��y����P����H3��H3Q��y����Q��
����H3Q=GP-CF=3-2 t-
t- t=3-3
t=3-3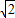 t��CQ=CP=3-2
t��CQ=CP=3-2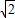 t��
t��
��OQ=OC+CQ=6-2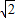 t��
t��
��H3��3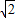 t-3��2
t-3��2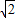 t-6����
t-6����
��H3���������ߵĽ���ʽ�У��У�
��3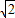 t-3��2-2��3
t-3��2-2��3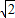 t-3��-3=2
t-3��-3=2 t-6��
t-6��
��9t2-13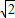 t+9=0��
t+9=0��
���t=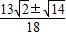 ��
��
��t=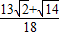 ʱ��H3��
ʱ��H3��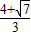 ��
��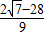 ����
����
��t=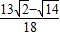 ʱ��H4��
ʱ��H4��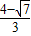 ��
��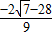 ����
����
�ʴ��ڷ���������H�㣬�ң�
��t=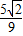 ʱ��H1��-
ʱ��H1��- ��-
��-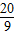 ����
����
��t=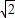 ʱ��H2��1��-4����
ʱ��H2��1��-4����
��t=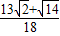 ʱ��H3��
ʱ��H3��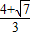 ��
��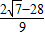 ����
����
��t=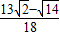 ʱ��H4��
ʱ��H4��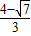 ��
��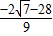 ����
����
���������⿼���˶��κ���ͼ���������ύ������������������ε��ж������ʡ�ƽ���ı��ε��ж�����Ҫ֪ʶ���ۺ���ǿ���ѶȽϴ����漰��������ʱ��һ��Ҫ���Ƿ�������˼������ã�
��2��������֪��A��B��C��D�����꣬��������������θ��Ե����߳���Ȼ��֤��BCD����AOC�Ķ�Ӧ�߳ɱ������ɣ�
��3������������������C��F��H��G�ĵ�Ϊ�����ƽ���ı��ε�H�����꣬Ȼ����������ߵĽ���ʽ�н�����֤���ɣ�
�ֱ��C��F��G��FG��CG��CF��ƽ���ߣ���ô��Щƽ���ߵĽ��㼴Ϊ�����H�㣬��ΪH1��H2��H3����G��GN��x����N�����ڡ�OBC=45°�����ɸ���BG�ij���ʾ��GN��BN��ֵ����CP�ij�����ã�����ƽ���ı��ε����ʣ�����Ա�ƽ������ȣ������ɵõ�H1��H2�����꣬Ȼ�����Ǵ��������ߵĽ���ʽ�н�����֤���ɣ������÷����н⣬�����õĽ⼴Ϊ����������H�����꣬���⣬����˵�������ڷ���������H�㣮H3��������ͬ�ϣ�
����⣺��1����y=0����x2-2x-3=0����x=3��x=-1��
��A��-1��0����B��3��0����
��x=0����y=-3��
��C��0��-3����
����y=x2-2x-3=��x-1��2-4��
�ʶ���D��1��-4����
��2�����ƣ��������£�
��A��-1��0����B��3��0����C��0��-3����D��1��-4����
��OA=1��OC=3��AC=
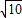 ��
��CD=
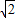 ��BC=3
��BC=3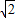 ��BD=2
��BD=2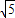 ��
����
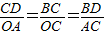 =
= ��
���ʡ�AOC�ס�DCB��
��3���ֱ��C��F��G��FG��CG��CF��ƽ���ߣ����߽���H1��H2��H3����ͼ����
���ı���CFGH1���ı���CFH2G���ı���H3FGC����ƽ���ı��Σ�
��G��GM��x����M��

����OB=OC=3�����OBC=45°��
��֪BG=4t����BM=MG=2
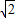 t��OM=3-2
t��OM=3-2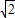 t��
t����G��3-2
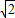 t��-2
t��-2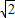 t����
t���������ı���CFGH1���ı���CFH2G����ƽ���ı��Σ�
��H1G=GH2=CF=
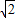 t��
t����H1��3-3
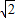 t��-2
t��-2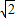 t����H2��3-
t����H2��3-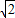 t��-2
t��-2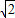 t����
t������H1���������ߵĽ���ʽ�еã�
��3-3
 t��2-2��3-3
t��2-2��3-3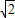 t��-3=-2
t��-3=-2 t��
t����9t2-5
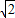 t=0��
t=0�����t=0����ȥ����t=
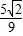 ��
����t=
 ʱ��H1��-
ʱ��H1��- ��-
��- ����
������H2���������ߵĽ���ʽ�еã�
��3-
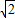 t��2-2��3-
t��2-2��3-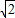 t��-3=-2
t��-3=-2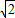 t��
t����t2-
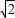 t=0��
t=0�����t=0����ȥ����t=
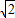 ��
����t=
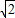 ʱ��H2��1��-4����
ʱ��H2��1��-4������G��GP��y����P����H3��H3Q��y����Q��
����H3Q=GP-CF=3-2
 t-
t- t=3-3
t=3-3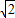 t��CQ=CP=3-2
t��CQ=CP=3-2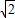 t��
t����OQ=OC+CQ=6-2
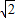 t��
t����H3��3
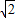 t-3��2
t-3��2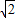 t-6����
t-6������H3���������ߵĽ���ʽ�У��У�
��3
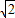 t-3��2-2��3
t-3��2-2��3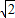 t-3��-3=2
t-3��-3=2 t-6��
t-6����9t2-13
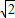 t+9=0��
t+9=0�����t=
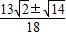 ��
����t=
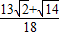 ʱ��H3��
ʱ��H3��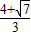 ��
��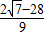 ����
������t=
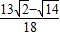 ʱ��H4��
ʱ��H4��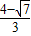 ��
��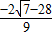 ����
�����ʴ��ڷ���������H�㣬�ң�
��t=
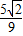 ʱ��H1��-
ʱ��H1��- ��-
��-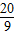 ����
������t=
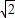 ʱ��H2��1��-4����
ʱ��H2��1��-4������t=
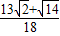 ʱ��H3��
ʱ��H3��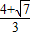 ��
��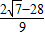 ����
������t=
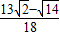 ʱ��H4��
ʱ��H4��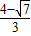 ��
��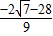 ����
�������������⿼���˶��κ���ͼ���������ύ������������������ε��ж������ʡ�ƽ���ı��ε��ж�����Ҫ֪ʶ���ۺ���ǿ���ѶȽϴ����漰��������ʱ��һ��Ҫ���Ƿ�������˼������ã�

��ϰ��ϵ�д�
 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
�����Ŀ
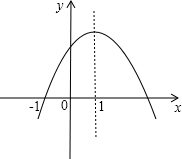 ��֪��ͼ������y=ax2+bx+c������ʽ�ӳ������ǣ�������
��֪��ͼ������y=ax2+bx+c������ʽ�ӳ������ǣ�������| A��a+b+c��0 | B��b��a+c | C��c��2b | D��abc��0 |
 ���ꣻ�������ڣ���˵�����ɣ�
���ꣻ�������ڣ���˵�����ɣ� ��l2������M�������Ծ�����A1B1�������������䣩����ô�����ܵ��ļ����������˻�����С�ˣ�˵�����ɣ�
��l2������M�������Ծ�����A1B1�������������䣩����ô�����ܵ��ļ����������˻�����С�ˣ�˵�����ɣ� ����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H��
����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H��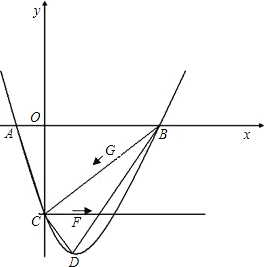 ���ꣻ�������ڣ���˵�����ɣ�
���ꣻ�������ڣ���˵�����ɣ�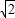 ����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�
����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�