题目内容
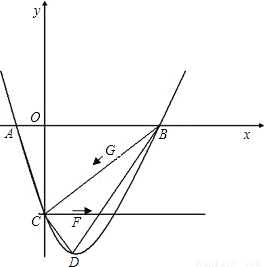
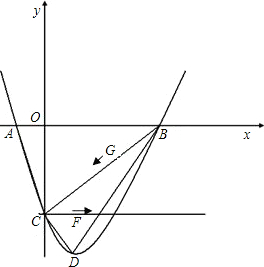
已知如图抛物线y=x2-2x-3与x轴交于A、B两点(A在B的左侧)与y轴交于C点,顶点为D.(1)求出A、B、C、D四点坐标;
(2)判断△AOC与△BCD是否相似,并说明理由;
(3)过C作直线CE平行x轴交抛物线另一个交点为E,动点F从C点开始,以每秒
| 2 |
 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
分析:(1)抛物线的解析式中,令y=0,可求得点A、B的坐标,令x=0,可求得点C的坐标;将抛物线的解析式化为顶点坐标式,即可求得点D的坐标.
(2)根据已知的A、B、C、D的坐标,可求得两个三角形各自的三边长,然后证△BCD、△AOC的对应边成比例即可.
(3)此题可先求出满足以C、F、H、G四点为顶点的平行四边形的H点坐标,然后代入抛物线的解析式中进行验证即可.
分别过C、F、G作FG、CG、CF的平行线,那么这些平行线的交点即为所求的H点,设为H1、H2、H3,过G作GN⊥x轴于N,由于∠OBC=45°,即可根据BG的长表示出GN、BN的值,而CP的长易求得,根据平行四边形的性质(两组对边平行且相等),即可得到H1、H2的坐标,然后将它们代入抛物线的解析式中进行验证即可,若所得方程有解,则所得的解即为符合条件的H点坐标,若无解,则是说明不存在符合条件的H点.H3的坐标求法同上.
(2)根据已知的A、B、C、D的坐标,可求得两个三角形各自的三边长,然后证△BCD、△AOC的对应边成比例即可.
(3)此题可先求出满足以C、F、H、G四点为顶点的平行四边形的H点坐标,然后代入抛物线的解析式中进行验证即可.
分别过C、F、G作FG、CG、CF的平行线,那么这些平行线的交点即为所求的H点,设为H1、H2、H3,过G作GN⊥x轴于N,由于∠OBC=45°,即可根据BG的长表示出GN、BN的值,而CP的长易求得,根据平行四边形的性质(两组对边平行且相等),即可得到H1、H2的坐标,然后将它们代入抛物线的解析式中进行验证即可,若所得方程有解,则所得的解即为符合条件的H点坐标,若无解,则是说明不存在符合条件的H点.H3的坐标求法同上.
解答:解:(1)令y=0,即x2-2x-3=0,则x=3,x=-1,
∴A(-1,0),B(3,0);
令x=0,即y=-3,
∴C(0,-3);
由于y=x2-2x-3=(x-1)2-4,
故顶点D(1,-4).
(2)相似,理由如下:
∵A(-1,0),B(3,0),C(0,-3),D(1,-4),
∴OA=1,OC=3,AC=
;
CD=
,BC=3
,BD=2
;
∴
=
=
=
,
故△AOC∽△DCB.
(3)分别过C、F、G作FG、CG、CF的平行线,三线交于H1、H2、H3(如图);
则四边形CFGH1、四边形CFH2G、四边形H3FGC都是平行四边形;
过G作GM⊥x轴于M;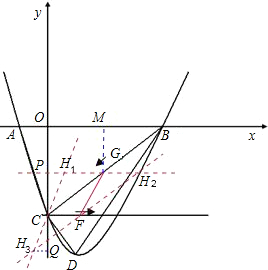
由于OB=OC=3,则∠OBC=45°;
易知BG=4t,则BM=MG=2
t,OM=3-2
t;
故G(3-2
t,-2
t);
由于四边形CFGH1、四边形CFH2G都是平行四边形,
故H1G=GH2=CF=
t,
∴H1(3-3
t,-2
t),H2(3-
t,-2
t);
把H1代入抛物线的解析式中得:
(3-3
t)2-2(3-3
t)-3=-2
t,
即9t2-5
t=0;
解得t=0(舍去),t=
;
当t=
时,H1(-
,-
);
把H2代入抛物线的解析式中得:
(3-
t)2-2(3-
t)-3=-2
t,
即t2-
t=0;
解得t=0(舍去),t=
;
当t=
时,H2(1,-4);
过G作GP⊥y轴于P,过H3作H3Q⊥y轴于Q;
则有H3Q=GP-CF=3-2
t-
t=3-3
t,CQ=CP=3-2
t;
∴OQ=OC+CQ=6-2
t;
∴H3(3
t-3,2
t-6);
将H3代入抛物线的解析式中,有:
(3
t-3)2-2(3
t-3)-3=2
t-6,
即9t2-13
t+9=0,
解得t=
;
当t=
时,H3(
,
);
当t=
时,H4(
,
).
故存在符合条件的H点,且:
当t=
时,H1(-
,-
);
当t=
时,H2(1,-4);
当t=
时,H3(
,
);
当t=
时,H4(
,
).
∴A(-1,0),B(3,0);
令x=0,即y=-3,
∴C(0,-3);
由于y=x2-2x-3=(x-1)2-4,
故顶点D(1,-4).
(2)相似,理由如下:
∵A(-1,0),B(3,0),C(0,-3),D(1,-4),
∴OA=1,OC=3,AC=
| 10 |
CD=
| 2 |
| 2 |
| 5 |
∴
| CD |
| OA |
| BC |
| OC |
| BD |
| AC |
| 2 |
故△AOC∽△DCB.
(3)分别过C、F、G作FG、CG、CF的平行线,三线交于H1、H2、H3(如图);
则四边形CFGH1、四边形CFH2G、四边形H3FGC都是平行四边形;
过G作GM⊥x轴于M;

由于OB=OC=3,则∠OBC=45°;
易知BG=4t,则BM=MG=2
| 2 |
| 2 |
故G(3-2
| 2 |
| 2 |
由于四边形CFGH1、四边形CFH2G都是平行四边形,
故H1G=GH2=CF=
| 2 |
∴H1(3-3
| 2 |
| 2 |
| 2 |
| 2 |
把H1代入抛物线的解析式中得:
(3-3
| 2 |
| 2 |
| 2 |
即9t2-5
| 2 |
解得t=0(舍去),t=
5
| ||
| 9 |
当t=
5
| ||
| 9 |
| 1 |
| 3 |
| 20 |
| 9 |
把H2代入抛物线的解析式中得:
(3-
| 2 |
| 2 |
| 2 |
即t2-
| 2 |
解得t=0(舍去),t=
| 2 |
当t=
| 2 |
过G作GP⊥y轴于P,过H3作H3Q⊥y轴于Q;
则有H3Q=GP-CF=3-2
| 2 |
| 2 |
| 2 |
| 2 |
∴OQ=OC+CQ=6-2
| 2 |
∴H3(3
| 2 |
| 2 |
将H3代入抛物线的解析式中,有:
(3
| 2 |
| 2 |
| 2 |
即9t2-13
| 2 |
解得t=
13
| ||||
| 18 |
当t=
13
| ||||
| 18 |
4+
| ||
| 3 |
2
| ||
| 9 |
当t=
13
| ||||
| 18 |
4-
| ||
| 3 |
-2
| ||
| 9 |
故存在符合条件的H点,且:
当t=
5
| ||
| 9 |
| 1 |
| 3 |
| 20 |
| 9 |
当t=
| 2 |
当t=
13
| ||||
| 18 |
4+
| ||
| 3 |
2
| ||
| 9 |
当t=
13
| ||||
| 18 |
4-
| ||
| 3 |
-2
| ||
| 9 |
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、相似三角形的判定和性质、平行四边形的判定等重要知识,综合性强,难度较大.在涉及动点问题时,一般要考虑分类讨论思想的运用.

练习册系列答案
相关题目
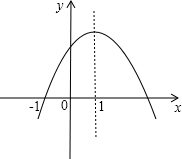 已知如图抛物线y=ax2+bx+c,下列式子成立的是( )
已知如图抛物线y=ax2+bx+c,下列式子成立的是( )| A、a+b+c<0 | B、b<a+c | C、c<2b | D、abc>0 |
 线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.
线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由. 个单位的速度沿CF方向在射线CE上运动,动点G从B点开始以每秒4个单位速度沿BC方向在射线BC上运动.设动点F、G同时出发运动时间为t,问在抛物线上是否存在点H;使以C、G、H、F四点为顶点的四边形为平行四边形?若存在,求出相应t的值和H的
个单位的速度沿CF方向在射线CE上运动,动点G从B点开始以每秒4个单位速度沿BC方向在射线BC上运动.设动点F、G同时出发运动时间为t,问在抛物线上是否存在点H;使以C、G、H、F四点为顶点的四边形为平行四边形?若存在,求出相应t的值和H的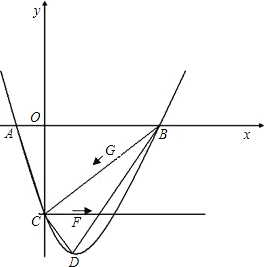 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.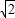 个单位的速度沿CF方向在射线CE上运动,动点G从B点开始以每秒4个单位速度沿BC方向在射线BC上运动.设动点F、G同时出发运动时间为t,问在抛物线上是否存在点H;使以C、G、H、F四点为顶点的四边形为平行四边形?若存在,求出相应t的值和H的坐标;若不存在,请说明理由.
个单位的速度沿CF方向在射线CE上运动,动点G从B点开始以每秒4个单位速度沿BC方向在射线BC上运动.设动点F、G同时出发运动时间为t,问在抛物线上是否存在点H;使以C、G、H、F四点为顶点的四边形为平行四边形?若存在,求出相应t的值和H的坐标;若不存在,请说明理由.