Question

【题目】如图，四边形ABCD为正方形，E为对角线BD上的动点，过点E作FG⊥AE，FG交射线CD于F，交射线CB于G．

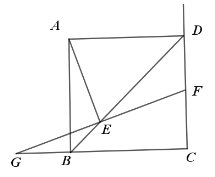
（1）求证：EF=EG

（2）求证：

（3）若AB=4，当∠GEB=22.5°，直接写出CF的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）如下图，先证△ABE≌△CBE，得出∠1=∠3，再通过角度转化，得出∠2=∠3和∠4=∠5，从而得出EF=EC=EG；

（2）如下图，先得出△GEH∽△GFC，根据相似三角形的线段成比例可求证；

（3）存在2种情况，一种是点F在线段CD上，另一种是点F在射线CD上，且在点D的上方，分别利用相似三角形和勾股定理可求得．

（1）证明：连接CE

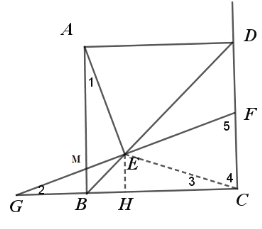
∵四边形ABCD为正方形

∴BA=BC，∠ABC=∠BCD=90°

∠ABE=∠CBE=45°

又∵BE=BE

∴△ABE≌△CBE(SAS)

∴∠1=∠3

又∵FG⊥AE

∴∠AEM=90°

∴∠1+∠AME=90°

又∵∠2+∠BMG=∠ABC=90° ∠AME=∠BMG

∴∠1=∠2

∴∠2=∠3

∴EG=EC

又∵∠3+∠4=90° ∠2+∠5=90°

∴∠4=∠5

∴EF=EC

∴EF=EG

（2）作EH⊥BC交BC于H

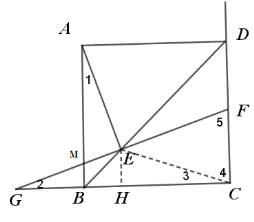
则∠GHE=90°=∠BCD

又∵∠2=∠2

∴△GEH∽△GFC

∴

∴FC=2EH=2×

（3）情况一：点F在线段CD上，图形如下

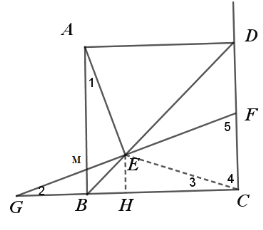
∵∠GEB=22.5°，BD是正方形ABCD的对角线

∴∠DBC=45°，∠BGE=22.5°

∴GB=BE

设BH=x，则HC=4－x

∴GB=HC－BH=4－2x=BE

∵CF=

∴CF=

∴EH=

在Rt△EBH中，

解得：x=4或x=4(舍)

∴CF=8

情况二：点F在射线CD上，且在点D的上方，图形如下，连接EC，过点E作EH⊥CD于点H

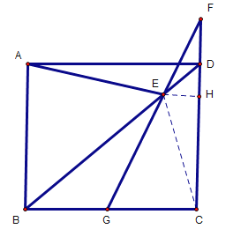
同理可得FC=

综上得；CF=．