题目内容
已知△ABC的周长是24cm，三边a、b、c满足c+a=2b，c-a=4cm，求a、b、c的长．
分析：隐形方程为a+b+c=24，然后再联立两方程得出方程组，解出a、b、c即可．
解答：解：由题意得，
，
解得：
．
即a、b、c的长度为6cm、8cm、10cm．
|
解得：
|
即a、b、c的长度为6cm、8cm、10cm．
点评：本题考查了三元一次方程组的应用，属于基础题，解答本题的关键是得出隐形方程a+b+c=24，难度一般．
练习册系列答案
相关题目
8、如图，已知△ABC的周长是34，其中AB=10，AO、BO分别是角平分线，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为（ ）已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为（ ）
| A、6 | B、8 | C、10 | D、12 |
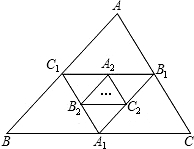如图：A1，B1，C1分别是BC，AC，AB的中点，A2，B2，C2分别是B1C1，A1C1，A1B1的中点…这样延续下去．已知△ABC的周长是1，△A1B1C1的周长是L1，△A2B2C2的周长是L2…AnBnCn的周长是Ln，则Ln=
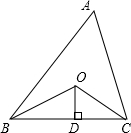如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是