题目内容
已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为
- A.2cm
- B.14cm
- C.2cm或14cm
- D.10cm或20cm
C
分析:本题要分类讨论:
(1)AB,CD在圆心的同侧如图(一);
(2)AB,CD在圆心的异侧如图(二).
根据勾股定理和垂径定理求解.
解答: 解:(1)AB,CD在圆心的同侧如图(一),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
解:(1)AB,CD在圆心的同侧如图(一),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
根据垂径定理得ED= CD=
CD= ×16=8cm,FB=
×16=8cm,FB= AB=
AB= ×12=6cm,
×12=6cm,
在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE= =
= =6(cm),
=6(cm),
在Rt△OFB中,OB=10cm,FB=6cm,则OF=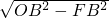 =
= =8(cm),
=8(cm),
AB和CD的距离是OF-OE=8-6=2(cm);
(2)AB,CD在圆心的异侧如图(二),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
根据垂径定理得ED= CD=
CD= ×16=8cm,FB=
×16=8cm,FB= AB=
AB= ×12=6cm,
×12=6cm,
在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE= =
= =6(cm),
=6(cm),
在Rt△OFB中,OB=10cm,FB=6cm,则OF=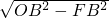 =
= =8(cm),
=8(cm),
AB和CD的距离是OF+OE=6+8=14(cm),
AB和CD的距离是2cm或14cm.
故选C.
点评:本题涉及到垂径定理及勾股定理,解题时要注意分类讨论,不要漏解.
分析:本题要分类讨论:
(1)AB,CD在圆心的同侧如图(一);
(2)AB,CD在圆心的异侧如图(二).
根据勾股定理和垂径定理求解.
解答:
 解:(1)AB,CD在圆心的同侧如图(一),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
解:(1)AB,CD在圆心的同侧如图(一),连接OD,OB,过O作AB的垂线交CD、AB于E,F,根据垂径定理得ED=
 CD=
CD= ×16=8cm,FB=
×16=8cm,FB= AB=
AB= ×12=6cm,
×12=6cm,在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE=
 =
= =6(cm),
=6(cm),在Rt△OFB中,OB=10cm,FB=6cm,则OF=
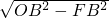 =
= =8(cm),
=8(cm),AB和CD的距离是OF-OE=8-6=2(cm);
(2)AB,CD在圆心的异侧如图(二),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
根据垂径定理得ED=
 CD=
CD= ×16=8cm,FB=
×16=8cm,FB= AB=
AB= ×12=6cm,
×12=6cm,在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE=
 =
= =6(cm),
=6(cm),在Rt△OFB中,OB=10cm,FB=6cm,则OF=
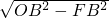 =
= =8(cm),
=8(cm),AB和CD的距离是OF+OE=6+8=14(cm),
AB和CD的距离是2cm或14cm.
故选C.
点评:本题涉及到垂径定理及勾股定理,解题时要注意分类讨论,不要漏解.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
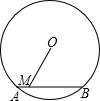 如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )
如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )| A、5 | B、7 | C、9 | D、11 |
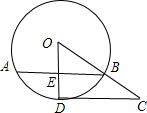 如图,AB为⊙O的弦,过点O作OD⊥AB于点E,交⊙O于点D,过点D作CD∥AB,连接OB并延长交CD于点C,已知⊙O的半径为10,OE=6.
如图,AB为⊙O的弦,过点O作OD⊥AB于点E,交⊙O于点D,过点D作CD∥AB,连接OB并延长交CD于点C,已知⊙O的半径为10,OE=6.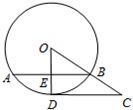 10,sin∠COD=
10,sin∠COD= 如图,已知⊙O的半径为
如图,已知⊙O的半径为