题目内容
16、已知⊙O的半径为10，P为⊙O内一点，且OP=6，则过P点，且长度为整数的弦有（ ）
分析：求出过P点的弦长的取值范围，取特殊解，根据对称性综合求解．
解答：
解：如图，AB是直径，OA=10，OP=6，过点P作CD⊥AB，交圆于点C，D两点．
由垂径定理知，点P是CD的中点，由勾股定理求得，PC=8，CD=16，则CD是过点P最短的弦，长为16；AB是过P最长的弦，长为20．所以过点P的弦的弦长可以是17，18，19各两条．总共有8条长度为整数的弦．
故选C．
解：如图，AB是直径，OA=10，OP=6，过点P作CD⊥AB，交圆于点C，D两点．由垂径定理知，点P是CD的中点，由勾股定理求得，PC=8，CD=16，则CD是过点P最短的弦，长为16；AB是过P最长的弦，长为20．所以过点P的弦的弦长可以是17，18，19各两条．总共有8条长度为整数的弦．
故选C．
点评：本题利用了垂径定理和勾股定理求解．注意在最短和最长的弦中的弦长为某一整数时有两条．
练习册系列答案
相关题目
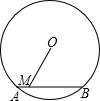如图，已知⊙O的半径为10，弦AB=12，M是AB上任意一点，则线段OM的长可能是（ ）| A、5 | B、7 | C、9 | D、11 |
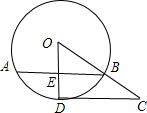如图，AB为⊙O的弦，过点O作OD⊥AB于点E，交⊙O于点D，过点D作CD∥AB，连接OB并延长交CD于点C，已知⊙O的半径为10，OE=6．
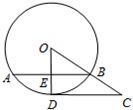10，sin∠COD=
如图，已知⊙O的半径为