题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,D是AB的中点,M是边AC上一点,连接DM,以DM为直角边作等腰直角三角形DME,斜边DE交线段CM于点F,若S△MDF=2S△MEF,则CM的长为_______.

【答案】![]()
【解析】
作DG⊥AC于G,EH⊥AC于H,则∠DGM=∠MHE=90°,DG∥BC,由勾股定理得出BC=6,证出DG是△ABC的中位线,得出DG=![]() BC=3,AG=CG=
BC=3,AG=CG=![]() AC=4,证明△MDG≌△EMH(ASA),得出MG=EH,由三角形面积关系得出DG=2EH=3,得出MG=EH=
AC=4,证明△MDG≌△EMH(ASA),得出MG=EH,由三角形面积关系得出DG=2EH=3,得出MG=EH=![]() ,求出AM=AG-MG=
,求出AM=AG-MG=![]() ,即可得出答案.
,即可得出答案.
作DG⊥AC于G,EH⊥AC于H,如图所示:

则∠DGM=∠MHE=90°,DG∥BC,
∵∠ACB=90°,AB=10,AC=8,
∴BC=![]() =6,
=6,
∵DG∥BC,D是AB的中点,
∴DG是△ABC的中位线,
∴DG=![]() BC=3,AG=CG=
BC=3,AG=CG=![]() AC=4,
AC=4,
∵△DME是等腰直角三角形,
∴∠DME=90°,DM=ME,
∵∠DMG+∠GDM=∠DMG+∠EMH=90°,
∴∠GDM=∠EMH,
在△MDG和△EMH中,
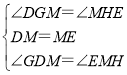 ,
,
∴△MDG≌△EMH(ASA),
∴MG=EH,
∵S△MDF=2S△MEF,
∴DG=2EH=3,
∴MG=EH=![]() ,
,
∴AM=AG-MG=4-![]() =
=![]() ,
,
∴CM=AC-AM=8-![]() =
=![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目